���꼉�σԔ��W�̰���ͨ��15ƪ��
��������һ��ĬĬ��I�Ľ��������ߣ�������Ҫ�M�н̰����������������̰������̌W�������ƌW������ô���}���ˣ��̰���ԓ��ô����������С�������ռ������꼉�σԔ��W�̰���ϣ�����������������
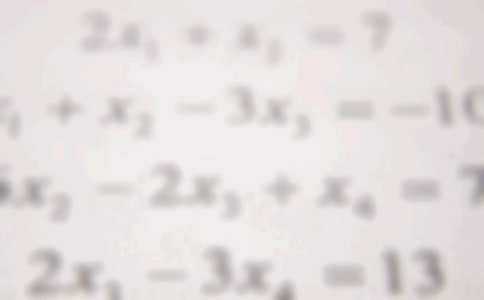
�������꼉�σԔ��W�̰� 1
����һ���̌WĿ��
������һ��֪�R�̌W�c
����1���˽⣻�������g�ⷨ�c�����ⷨ�ą^�e��
����2�����գ������ⷨ�⺆���̡�
��������������Ӗ���c
����1��ͨ�^�����ⷨ�⺆���̵ČW��ʹ�W���J�R���}�^�X�����������B�䄓����˼�S��������
����2��ͨ�^�������⺆�����Mһ�����B�W���\��������߉˼�S������
���������������B�c
����1�����B�W���������ǵĿƌW�B�ȣ��ðlչ���۹⿴���}���q�CΨ�����x˼�롣
����2���B����δ֪���顰��֪���Ļ��w˼�롣
�������ģ������B�c
����ͨ�^���µķ����⺆���̣�ʹ�W�������I�Ԕ��W�еķ�������
���������W������
����1���̌W�����������l�F����ע��̌W���������R�͌W�������w���õ��w�F��
����2���W���W�����Rӛ����������
�����������c���y�c�����c����Q�k��
����1�����c�������ⷨ�⺆���̡�
����2���y�c���ⷽ�̕r�ʴ_���Ճ�߅�����ϣ���pȥ�������ԣ�����ԣ�ͬһ�m���Ĕ���
����3�����c�������ⷨ�⺆���̵�������
�����ġ��n�r����
����1�n�r
�����塢�̾ߌW�ߜʂ�
����ͶӰ�x����X�������zƬ��
���������������ӻ���OӋ
�����̎����O�龳���W����Q���}���̎���B�µ�'�������W�����;�����
�����ߡ��̌W���E
������һ�����O�龳����������
��������ʾͶӰ1��
����������������37��ͬ�W���ֳ��˔���ȵă���M�аκӱ�ِ��ǡ����3�ˮ����ІT��ÿ����ж����ˣ�
��������ԓ���}��ν�Q�أ�Ոͬ�W�����]�ú��ھ������ϡ�
�����W����ӣ�������}��һ���W�����ݡ�
����������ͬӆ�������հ��W�����������������Пo��ͬ�ⷨ��
�����W����ӣ��ش����}��һ���W�����ݣ������W�����^�ɷN�ⷨ��
���������@�ɷN�ⷨ��ʲô��ͬ�أ�
�����W����ӣ��e�O˼�����ش����}����һ������ʽ�Ľⷨ�������з��̵Ľⷨ����
���������ܺá����˔������}���㣬�҂��քe���@�ɷN�ⷨ�������g�ⷨ�ʹ����ⷨ��С�W�W�^�đ����}�������g����Ҳ���ô��������⡢�Еr���g�������㣬�Еr�����������㣬�����S���W������չ�_�������Ć��}Խ��Խ���s��ʹ�ô����ⷨ�ă�Խ�Ԍ����w�F��Խ��Խ��֣���ˣ��ڳ��д����n�ϣ����ѷ��̵�֪�R����һ����Ҫ�ă��݁�W������Ȼ�����_ʼ�W�����̕r��߀��Ҫ�ĺ��εķ������֣��������̡������n�}��
����[���]1��5������
����������̽����֪���v�����n
��������Մ�����̣�ͬ�W������İ���������f��ʲô�з��̆
�����W����ӣ��x�S�e�֣��ش����}��
����[���]����δ֪���ĵ�ʽ�з���
�����ӆ�����߀֪���P�ڷ��̵���������
�����W����ӣ��e�O˼�����ش�
����[���]���̵Ľ⣻�ⷽ��
�����������پ��wЩ���ʲô�з��̵Ľ⣿ʲô�нⷽ�̣����e���f�����W����ӣ�����ӑՓ��ش𡢣�ʹ�������҃�߅��ȵ�δ֪����ֵ�������̵Ľ⣻�̵Ľ���^�̽нⷽ�̡�
���������ã��@��С�W�W�Ľⷽ�̵ķ������ڳ��д����n�ϣ��҂�Ҫ����һ�Ƕȁ��⣬߀����߅�@�����̞�����
����[���]
�����W����ӣ��ӑՓ�_�ɹ��R�����������x=5���뷽��3x+9=24����߅=��߅������x=5�Ƿ��̵Ľ⣩
�������꼉�σԔ��W�̰� 2
����һ�����픵�����x
����1�����픵�ķ��
����֪�R�c��������Ĕ���������������ǰ����ϡ��������x��ؓ��̖�Ĕ���ؓ�������һ��������ʾһ�������������ô���ϡ�����̖���@������������ȫ�෴�����x��3��5.2Ҳ�Ɍ���+3��+��+5.2����Ȳ���������Ҳ����ؓ����
����2�����S
����֪�R�c�����S�ǔ��c�D�νY�ϵĹ��ߣ����S��Ҏ����ԭ�c��������͆�λ�L�ȵ�ֱ�������S����Ԫ�أ�ԭ�c��������λ�L�ȣ��@��Ԫ��ȱһ���ɣ����Д�һ�lֱ���Ƿ��ǔ��S�ĸ������������S�����ã�1������ر�ʾ����������е����픵�������Ô��S�ϵ��c��ʾ���Ժ��֪�����S�ϵ�ÿһ���c��������ʾ���픵����2��ͨ�^���S�ĈD���Ͽ�ֱ�^�ؽ���෴������������^��ֵ�����x��3�����^���픵�Ĵ�С��a����߅�Ĕ�������߅�Ĕ���b�������������㣬c��ؓ����С���㣬d����������һ��ؓ��
����3���෴��
����֪�R�c��ֻ�з�̖��ͬ�ăɂ��������෴�����ڔ��S�ϱ�ʾ�����෴���ăɂ��c��ԭ�c�ľ��x����ҷքe��ԭ�c��.��߅��Ҏ����0���෴����0��
����4���^��ֵ
����֪�R�c��һ����a�Ľ^��ֵ���ǔ��S�ϱ�ʾ��a���c�cԭ�c�ľ��x����a�Ľ^��ֵӛ���Oa�O���^��ֵ�����x��һ�������Ľ^��ֵ����������һ��ؓ���Ľ^��ֵ�������෴������Ľ^��ֵ���㣬����a>0���t�Oa�O=a����a=0���t�Oa�O=0����a<0���t�Oa�O=��a���^��ֵԽ���ؓ������С���ɂ��ca�cb֮�g�ľ��x�飺�Oa��b�O��
�����������픵���\��
����1�����픵�ļӷ�
����֪�R�c�����픵�ļӷ����t��
����1��̖ͬ�ɔ���ӣ�ȡ��ͬ�ķ�̖�����ѽ^��ֵ��ӣ�
����2����̖�ɔ���ӣ��ٽ^��ֵ��ȕr���͞��㣨�������෴���ăɂ�����ӵ�0�����ڽ^��ֵ����ȕr��ȡ�^��ֵ�^��ķ�̖�������^��Ľ^��ֵ�pȥ�^С�Ľ^��ֵ��
����3��һ������0����Ե��@������
�����ӷ����Q�ɣ�a+b=b+a���ӷ��Y���ɣ�a+b+c=a+��b+c��
�����������픵��ӕr���ѷ�̖��ͬ�Ĕ��Y����һ��Ӌ����^���㣬���л����෴�Ĕ��������������ĺ͞�0�����c��
����2�����픵�Ĝp��
����֪�R�c�����픵�Ĝp�����t���pȥһ�������ڼ����@�������෴������a��b=a+����b����
����ע�⣺�\���̖��+����̖���������p̖�c���|��̖��+����̖��������̖ؓ�yһ�c�D������a��b�еĜp̖Ҳ�ɿ���̖ؓ������a�cb���෴���ĺͣ�a+����b����һ�����pȥ0���Ե��@������0�pȥһ�����������@�������෴����
����3�����픵�ļӜp����\��
����֪�R�c�����픵�ļӜp������\������\�Üp�����t�yһ�ɼӷ��\�㣻�Ӝp������\��yһ�ɼӷ��\���Ժ��ѡ�+��̖ʡ�ԣ�ʹ��ʽ׃�ø��Ӻ�����
����4�����픵�ij˷�
����֪�R�c���˷����t���ɔ���ˣ�̖ͬ��������̖��ؓ�����ѽ^��ֵ��ˣ��κΔ���0��˶���0��
�����ׂ�������0�Ĕ���ˣ��e�ķ�̖��ؓ�Ă����Q������ؓ�����攵���r���e��ؓ����ؓ����ż�����r���e�������ׂ�����ˣ���һ����0���e�͞�0��
�����˷����Q�ɣ�ab=ba�˷��Y���ɣ�abc=a��bc���˷������ɣ�a��b+c��=ab+bc
����5�����픵�ij���
����֪�R�c���������t1������һ�������ڳ����@���ĵ�������a��b==a��b��0��0��������������
�����������t2���ɔ������̖ͬ��������̖��ؓ�����ѽ^��ֵ�����0�����κ�һ��������0�Ĕ�����0��
�����������˷e��1�ăɔ����鵹������a=1��a��0����0�]�е�����
����ע�⣺�����c�෴���ą^�e
����6�����픵�ij˷�
����֪�R�c���˷�����n����ͬ�ķe���\�㡣�˷��ĽY���Ѓ磬an�У�a�����ה���n����ָ����
�����˷��ķ�̖���t���������κδ綼��������ؓ���������ؓ����ؓ����ż����������0���κδ綼��0��
����7�����픵�Ļ���\��
����֪�R�c���\������ȳ˷����ٳ˳��������Ӝp����������̖������С��̖��������̖��������̖���ж�����̖�r���������������M�С�
�������ɣ����^����ʽ�ĽY�����߄����\������`���M���\�㡣
�������꼉�σԔ��W�̰� 3
�������ݣ�
������ʽ�ij˷������ʽ���Զ��ʽP58-59
�����n�ͣ�
�������ڕr�g��
�����W��Ŀ�ˣ�
����1���ھ��w�龰�У��˽���ʽ�Ͷ��ʽ��˵����x��
����2����ͨ�^�W������У�������ʽ�Ͷ��ʽ��˵ķ��t�����������M��Ӌ�㡣
����3�����B�W���Зl����˼���ͱ��_������
�����W�����c��
�������ʽ���Զ��ʽ�ķ��t
�����W���y�c��
���������t������
�����W���^�̣�
����1���W���ʂ�
����1.�������ʽ���Ԇ��ʽ�ķ��t
����2.Ӌ��
����(1)(-a2b)?(2ab)3=
����(2)(-2x2y)2?(-xy)-(-xy)3?(-x2)
����3���e���f���˷������ɵđ��á�
����2������̽��
������һ������˼������Q���}
����1�����}��һ��ʩ�������һ�l·�挒��nm��`��·����һ������am�L���ڶ��������Lbm�������������Lcm��3�칤����·�����e�Ƕ��٣�
�����Y�ψD�Σ������ա�
�����㷨һ��3�칲����·��Ŀ��L�飨a+b+c��m�����·��Č���bm������3
�����칲����·��m2.
�����㷨�����ȷքeӋ��ÿ������·�����e��Ȼ����ӣ��t3����·��m2.
������ˣ���=��
����3.��������ĸ��ʾ�˷������Ɇ
����4.���܇Lԇ���ʽ���Զ��ʽ�ķ��t�
��������������̽������������
����1����3Ӌ�㣺
������1��(-2x)(-x2?x+1)��2��a(a2+a)-a2(a-2)
����2����һ��
������1��5x(3x+4)(2)(5a2?a+1)(-3a)
����(3)x(x2+3)+x2(x-3)-3x(x2?x-1)
����(4)(?a)(-2ab)+3a(ab-b-1))
�����������W��
�������ՌW��Ŀ�ˣ�ͨ�^�A�������X���Լ�����Щ������ի@����ʲô�ɻ�
�������ģ����Ҝyԇ
����1���̿ƕ�P59����3���Y�Ͻ��}�����ʽ���Զ��ʽ�Ď����x��
����2�����}
����(1)-2a(3a-4b)=-6a2-8ab()
����(2)(3x2-xy-1)?x=x3-x2y-x()
����(3)m2-(1-m)=m2--m()
����3����֪ab2=-1,-ab(a2b3-ab3-b)��ֵ���ڣ���
����A.-1B.0C.1D.�o���_��
����4��Ӌ�㣨2009�R���п���
������-2a��?(a3-1)=
����5��(3m)2��m2+mn-n2��=
�������壩������չ
����1��Ӌ��
����(1)2a��9a2-2a+3��-(3a2)?(2a-1)
����(2)x��x-3��+2x(x-3)=3(x2-1)
����2����һ�����ε��ϵ��L��4m+3n��cm���µ��L��2m+n��cm���ߞ�3m2ncm��������ε���e��
����3��һ�K߅�L��xcm�������εشu������Ҫ���õ�һ�K2cm�����L�l����ʣ�²�����e�Ƕ��٣�
�������꼉�σԔ��W�̰� 4
����һ��֪�R�c����
�������Д�һ����������߀��ؓ��������������ؓ����ʾ�����о����෴���x������
���������^���c����
�������������еČ����������픵�����x���w��ؓ������ı�Ҫ�Ժ����픵���õďV���ԡ�
����������БB���c�rֵ�^
�������B�W���e�O˼�����������������R��������
�����̌W�ء��y�c�c�P�I
����1�����c�����_����ؓ�������x�������Д�һ����������߀��ؓ���ķ�����
����2���y�c�����_����ؓ���ĸ��
����3���P�I�����O�龳��������ÌW����߅��Ϥ��������ؓ�����x�����⡣
�����̾ߜʂ�
����ͶӰ�x��
�����̌W�^��
�����ġ��n������
�����҂�֪���������˂��ڌ��H�����������Ҫ�Юa�����������U��ġ��˂���ӛ�������a����1��2��3���������˱�ʾ���]�����w��������λ�����M�˔���0�����y���ͷ����Еr���ܵõ������ĽY������ˮa���˷֔���С����
������������a�������н����������ı�ʾ�c�����\��Ć��}�������n����2�����3����ᵽ���Ă����}���@����F��������3����2����2.7%��ǰ��Č��H���}�������քe��ʾ������3�z�϶ȣ���ݔ2�p��2.7%��
�����塢�v�����n
������1������3����2����2.7%�@�ӵĔ���������ǰ�W�^��0����Ĕ�ǰ�����̖ؓ�������Ĕ�������ؓ������3��2��+2.7%�چ��}�зքe��ʾ����3�z�϶ȣ����2�����L2.7%�������cؓ�������෴�����x���҂����@�ӵĔ�������ǰ�W�^��0����Ĕ��������������Еr������ǰ��Ҳ���ϡ�+��������̖�����磬+3��+2��+0.5��+��������3��2��0.5����һ����ǰ��ġ�+����������̖�������ķ�̖���@�N��̖�������|��̖��
������2�����Ї��Ŵ�����I����ʾ���Ĺ��ߣ��M��Ӌ�㣬�tɫ��I��ʾ��������ɫ��I��ʾؓ����
������3������0�Ȳ���������Ҳ����ؓ������0�������cؓ���ķֽ电��
������4����0���Ա�ʾ�]�У�߀���Ա�ʾһ���_�����������������0�棬��ָһ���_���Ĝضȣ�����0��ʾ��ƽ���ƽ���߶ȡ�
��������ؓ����ʾ�����෴���x����
������5������0����Ĕ��֞�������ؓ������Դ�ڱ�ʾ�ɷN�෴���x������������ؓ�����S��汻�V���ؑ��á��ڵ��ΈD�ϱ�ʾij�ظ߶ȕr����Ҫ�Ժ�ƽ�����ʣ�ͨ����������ʾ���ں�ƽ���ij�صĺ��θ߶ȣ�ؓ����ʾ���ں�ƽ���ij�صġ����θ߶ȡ����磺�����ʬ����.���θ߶Ȟ�8844m����������صĺ��θ߶Ȟ顪155m��ӛ��~Ŀ�r��ͨ����������ʾ������~��ؓ����ʾ֧�����~��
������6����Ո�W������n���ЈD1.1��2���D1.1��3�е�������ؓ���ĺ��x��
������7�����������eһЩ����ؓ����ʾ�����Č��H���ӆ
������8�������磬ͨ����������ʾ��܇��|����·�̣���ؓ����ʾ��܇��������·�̣���������ʾˮλ���ߵĸ߶ȣ���ؓ����ʾˮλ�½��ĸ߶ȣ���������ʾ�I�M�|���Ĕ�������ؓ����ʾ�u���|���Ĕ�����
��������얹̾���
�����n����3퓣�����1��2��3��4�}��
�����ߡ��n��С�Y
�������˱�ʾ�F�������еľ����෴���x�������҂����M��ؓ�������������҂��^ȥ�W�^�Ĕ�����0�⣩��������ǰ���ϡ�����̖������ؓ�����������f��������̖�Ĕ�����������̖ؓ�Ĕ���ؓ��������һ����ǰ������̖ؓ������ʾ����ԭ�����x�෴�Ĕ������ԭ����һ��ؓ������ôǰ����ϡ�����̖������ʾ�Ĕ������������ˣ����⑪ע�⡰0���Ȳ���������Ҳ����ؓ����
�����ˡ����I����
����1���n����5����}1.1����얹̵�1��2��3�}��
�������꼉�σԔ��W�̰� 5
�����̌WĿ�ˣ�
����֪�R�������������픵�ĸ���������픵�ăɷN��������܉�Ҫ�o�������픵�M�з��
�����^���c������ͨ�^�����ČW�������B�W�����_�ķ��ӑՓ�^�c�ͷ��������
������С��B�ȡ��rֵ�^��ͨ�^�����n�ČW�����w�ɹ���ϲ�������W�Ô��W�����ġ�
�����̌W���c��
�����������픵�ăɷN�����
�����̌W�y�c��
�����o���Ĕ��������������ٵļ�����
�����̌W������
�������}����
�����W��������
��������̽����
�����̌W�^�̣�
����һ���΄ݚw�{
����С�W�҂��W�������ͷ֔����Ϲ��n�҂��W��������ؓ�����l�ܿ�����������}��
�����������֣�15����1/9����5��2/15����13/8��0.1����5.22����80��0��123��2.33
������1�������ϔ����������ɽM����������{}��ؓ������{}���������ˆ
������2�������ϔ����������ɂ����ϣ���������{}�ͷ֔�����{}���������ˆ
�����Q�����ͷ֔������픵����ָ�c�}�������
���������ԌWָ��
�����W���ԌW�n���������n�������ԌW�ęC��
������V�І��}�Ĵ𰸣��ώ�������Ҫ��`����ʂ䣬�ٵ��W����Ѳҕָ�������˽����ՌW���ԌW��r����չʾ�w�{���ʂ䡣
��������չʾ�w�{
����1�����І��}�ČW�����}չʾ�ԌW��V�еĆ��}�𰸣��W���f���ώ������
����2���l�ӌW���M���u�r���a�䡢���ƣ��̎�����ÿ���}Ŀ��չʾ��r�M�б�Ҫ���v��͏��{��
����3��ȫ��չʾ�ꮅ���ώ�������֪�R��ϵ�y�������P�I�c���ԏ��{��
�����ġ�׃ʽ����
�������}��ʾ�����W��������ɣ���Ո�І��}�ČW���R��Y�����ώ���������l�������W���u�r���a�䲢���ƣ�����ώ�������Ҫ�M�����c���{��
�����塢���Y�c��˼��ͨ�^�����n�ČW��������ʲô�ի@��
�����������I�������}���n��14퓣�1��9�}
�������꼉�σԔ��W�̰� 6
�������W��Ŀ�ˡ���
����1������������ؓ�����
����2�����^�փɷN��ͬ���x���������÷�̖��ʾ������ؓ����
����3���w�W�lչ������H����Ҫ�����l�W���W�����W���dȤ��
���������c�y�c����
����������ؓ������
�������̌W�^�̡���
����һ��֪�R朽ӣ�
����1��С�W��W�^��Щ��Ո��������
����2����x�n��P2�����D�����c���������ӣ�߅��x߅˼�����ش���������Ć��}��
����3���������У��H�������ͷ֔������ˆ�Л]�б�0С�Ĕ�������У��ǽ���ʲô����
�������������W��
����1�������cؓ���Įa��
������1���������о����෴���x����
�����磺�\�M5���c�\��3��������7���c�½�8�ף���|50���c����47�ȶ��������������ľ����෴���x������Ո��Ҳ�eһ�������෴���x�������ӣ���
������2��ؓ���Įa��ͬ������������a����Ҫ
����2��������ؓ���ı�ʾ����
������1��һ��أ��҂����������\�M�����ϡ����롢ǰ�M���߳���Ҏ�������ģ����c���෴�������磺�½����\�������¡�֧�������ˡ����ڵ�Ҏ����ؓ�ġ�����������С�W��W�^�Ĕ���ʾ���ЕrҲ����ǰ�����һ����+�����x������̖����ǰ���5��7��50��ؓ������С�W�W�^�Ĕ�ǰ����ϡ��������x��ؓ��̖����ʾ���������`��3����8����47��
������2����ӣ��ɂ�ͬ�W��һ�M��һͬ�W�����f���x�෴�ăɂ�������һ��ͬ�W����ؓ����ʾ.
������3����xP2���
����3��������ؓ���ĸ���
����1������0�Ĕ�������С��0�Ĕ�������
����2�������Ǵ���0�Ĕ���ؓ���ǵĔ���0�Ȳ�������Ҳ����ؓ����
�������n�þ�������
����1��P3��1��2�}��ֱ�������n���ϣ���
����2��С���Ľ�����y�й��������Ѵ���3�fԪӛ��+3�fԪ����ô֧ȡ2�fԪ��ӛ��_______,-4�fԪ��ʾ________________��
����3����֪���и�����?13��?2��3.14��+3065��0��-239��54
�����t������_____________________��ؓ����____________________��
����4�����нYՓ�����_����????????????????����
����A��0��������������ؓ��
����C��0������ؓ��
������Ҫ�c�w�{����
����������ؓ���ĸ��
������1������0�Ĕ�������С��0�Ĕ�������
������2�������Ǵ���0�Ĕ���ؓ���ǵĔ���0�Ȳ�������Ҳ����ؓ����
��������չӖ������
����1������15�棬��ʾ��_________����O���4��Ĝض���_________��
����2���؈D�Ϙ��мغ��θ߶�30�ף��ҵغ��θ߶Ȟ�20�ף����غ��θ߶Ȟ�-5�ף�
�����������̎��_______�أ����̎��_______�ء�
����3�����ױ��Ҵ�-3�q����ʾ�����x��______________________��
����4�������ƽ��ĸ߶Ȟ�0�ף�һ��ˮͧ�ں�ˮ��40��̎���У�һ�l���~�ڝ�ˮͧ�Ϸ�10��̎�΄ӣ�ԇ����ؓ���քe��ʾ��ˮͧ�����~�ĸ߶ȡ�
�������n�����I��P5��1��2�}
�������꼉�σԔ��W�̰� 7
�����̌WĿ��
����1���˽�һԪһ�η��̵ĸ��
����2�����պ�����̖��һԪһ�η��̵Ľⷨ��
�������c���y�c
����1�����c���⺬����̖��һԪһ�η��̵Ľⷨ��
����2���y�c����̖ǰ����̖ؓ�r��ȥ��̖�r��ӛ׃̖��
�����̌W�^��
����һ�������ᆖ
����1�������з��̣�
������1��5x��2=8��2��5+2x=4x
����2��ȥ��̖���t��ʲô������헡�Ҫע��ʲô��
������������
����һԪһ�η��̵ĸ��
������44x+64=3283+x=��45+x��y��5=2y+1����������ʲô��ͬ������
����ֻ����һ��δ֪�������Һ���δ֪����ʽ�Ӷ�����ʽ��δ֪���ĴΔ���1���@�ӵ�.���̽���һԪһ�η��̡�
������1���Д�������Щ��һԪһ�η���
����x=3x��2x��=��1
����5x2��3x+1=02x+y=1��3y=5
������2���ⷽ�̣�1����2��x��1��=4
������2��3��x��2��+1=x����2x��1��
�������{ȥ��̖�r����̖����քe������̖�ȵ�ÿһ헣�����̖ǰ���ǡ�����̖��ע��ȥ����̖��Ҫ��׃��̖�ȵ�ÿһ헵ķ�̖��
�����a�䣺�ⷽ��3x��[3��x+1������1+4��]=1
�����f�����������ж�����̖�r��һ�㑪����ȥС��̖����ȥ����̖�����ȥ����̖�ķ���ȥ��̖��ÿȥһ����̖�ϲ�ͬ��һ�Σ��Ժ����\�㡣
��������얹̾���
�����̿ƕ���9퓣�������1��2��3��
�����ġ�С�Y
�����W����һԪһ�η��̵ĸ��������̖��һԪһ�η��̵Ľⷨ���÷�����ȥ��̖�r����Ҫ©����̖�е�헣����Ҳ�Ҫ���e��̖��
�����塢���I
����1���̿ƕ���12����}6��
����2����1�}��
�������꼉�σԔ��W�̰� 8
�������̌WĿ�ˡ�
����֪�R�c���ܣ��˽Ⲣ���Ք����ռ��Ļ���������
�����^���c���������{����^���У�Ҫ���J��đB�ȣ��e�O���c��
������С��B���c�rֵ�^���w���yӋ�{���ڽ�Q���H���}�е����ã����B���Ô����fԒ���������T��
�������̌W���y�c��
�������c�����սyӋ�{��Ļ���������
�����y�c���ܸ������H��r�������x���{�鷽����
�������̌W�^�̡�
�����v�����n
������ǰ���ᵽ���ռ������Ļ���У�ȫ��ͬ�W���҂�Ҫ����Č����҂����Æ��팦ȫ�wͬ�W������һ�{�飬���@�ӌ�ȫ�w�����M�е��{�����ȫ���{�顣
�����{�顢ԇ�������ղ�����ռ����^ȫ�桢�ʴ_�Ĕ��������ղ�Ĺ��������^���Еr�ܿ��^�l����������ؔ���ȣ��������y���M�У��Еr�����{������Ɖ��ԣ������S���á����@Щ��r�£��������ó���{�飬���ı������ȫ�w�����г��һ�������M�п�����{�鷽ʽ��
������һ���yӋ���}�У��҂�����Ҫ���쌦���ȫ�w�������w�����е�ÿһ�����쌦��������w���Ŀ��w������ȡ��һ���ւ��w�������w��һ���ӱ���sample�����ӱ��Ђ��w�Ĕ�Ŀ�����ӱ�������
�������磬��ͨ�^ԇ��500ֻ�¹�ˇ���a�ğ��ݵ�ʹ�É����r�����г�ȡ50ֻ�M��ԇ�@500ֻ���ݵ�ʹ�É�����ȫ�w�ǿ��w������ÿֻ���ݵ�ʹ�É����ǂ��w����ȡ��.50ֻ���ݵ�ʹ�É�����һ���ӱ���50���@���ӱ��Ęӱ�������
��������ʹ��ȡ��50ֻ�����ܺܺõط�ӳ500ֻ���ݵ���r����ȡ�rҪʹÿֻ������һ�M�о�̖���ٰѾ�̖����С��Ƭ�ϣ���С��Ƭ��ɈF������һ�������������ȣ���֔������һ�����س�ȡ50��̖����
���������ȡ�ӱ����^���У����w�еĸ������w������ȵęC�����鵽�����@�ӵij�ӷ�����һ�N�����S�C��ӡ�
���������ԡ���֪����ĸ�����Ն�����}�ڰ༉�M���{�飬Ո�OӋһ�������{�����
�����W��С�M������ӑՓ���W������չʾ�Y����
�����̎�ָ�����uՓ��
�����������ˆ����{���⣬�҂�߀����Щ�����ռ��������أ�
�����W��С�MӑՓ���������W�������ش�
���������ռ�������ֱ�ӷ������L�����{�顢�^�졢�y����ԇ�ȣ��g�ӷ����в���Y�ϡ��ϾW��ԃ�ȡ������½yӋ�Ĕ��������J���x��ηN����ȥ�ռ����^���m��
������1������е�ͬ�W����ΰ�����ĩ�r�g�ģ�
������2���҇��l�R��^��ֲ�����
������3��ij�N���N�ӵİlѿ�ʣ�
������4���WУ�T��ʮ��·��ÿ��7��00~7��10�r��܇������
�������꼉�σԔ��W�̰� 9
�����̌WĿ�ģ�
����(һ)֪�R�cĿ�ˣ�
����1���˽�������ؓ�������Ӯa���ġ�
����2��֪��ʲô��������ؓ����
����3�����┵0��ʾ���������x��
����(��)����Ӗ��Ŀ�ˣ�
����1���w�����W��̖�c������˼�룬������ؓ����ʾ�����෴���x�����ķ�̖��������
����2����������ؓ����ʾ�����෴���x������
����(��)����c�rֵ�^Ҫ��
����ͨ�^����������ϵ���H�����l�W���W�Ô��W�ğ��顣
�����̌W���c��
����֪��ʲô��������ؓ�������┵0��ʾ���������x��
�����̌W�y�c��
��������ؓ������0��ʾ���������x��
�����̌W������
�������������c�̎��v����Y�ϡ�
�����̾ߜʂ䣺
�����؈D��(�Ї����ΈD)��
�����̌W�^�̣�
�����������n��
������ӣ��ɃɽM���Ƀ���ͬ�W�M�����»�ӣ�һ�����ώ���ָ����ݣ���һ���ںڰ�����ӛ������һ�Mӛ����졢?
�������ݣ��ώ��f��ָ�
������ǰ�ɲ������ɲ�;
������ǰһ�����������;
������ǰ�ɲ������һ��;
������ǰ�IJ������ɲ���
��������W�����������̖��ʾ���̎��ɺ�һ��С�M�������÷�̖��ʾ��+2��-2��+1��-3��+2��-1��+4��-2�ȡ�
����[��]�䌍�����҂��������У��\���@�ӵķ�̖�ĵط��ܶ࣬�@���n���҂��́�W���@�N���������̖����ʾ���Ќ��H���x��.��-----������ؓ����
�����v�����n��
����1����Ȼ���Įa�����֔��Įa����
����2�����^�D�����}Ҋ�̲ġ��W��˼��-3~3�桢������c�������0.5��-9�����x��
����3��������ؓ���Ķ��x���҂�����ǰ�W�^��0����Ĕ��������������@Щ����ǰ�控�С�һ���r����ؓ����������Ҫ�Еr������ǰ��Ҳ���ϡ�ʮ��(��̖)��ʾ������
�����e���f����3��2��0.5����������(Ҳ�ɼ��ϡ�ʮ��)
����-3��-2��-0.5��-����ؓ����
����4����0�Ȳ�������Ҳ����ؓ����0��������ؓ���ķֽ硣
����0����һ���_���Ĝضȣ����Ξ�0�ĸ߶��Ǻ�ƽ���ƽ���߶ȣ�0�����x�Ѳ��H��ʾ���]�С���
����5���W���e���f������ؓ���ڌ��H�еđ��á�չʾ�DƬ(��Ҋ�̲�P5�D1.1-2-3)�W���^����ΈD�ϵĘ�ע��ӛ�֧����������Ϣ�ı���X�y�еĴ��ۣ��f����֪������Ϣ��
����얹���ߣ��������n��P5����
�����n�rС�Y���@���n�҂��W������Щ֪�R?�����fһ�f��?
�����n�����I���n��P7���}1.1�ĵ�1��2��4��5�}��
��������c̽������һ�Δ��W�y��У�X���ƽ���֞�85�֣��Ѹ���ƽ���ֵĸ߳�����ӛ��������
����(1)������95�֣���ӛ�����?
����(2)��౻ӛ��һ12�֣������H�÷��Ƕ���?
�������꼉�σԔ��W�̰� 10
�����̌WĿ��
����1���˽�һԪһ�η��̵ĸ��
����2�����պ�����̖��һԪһ�η��̵Ľⷨ��
�������c���y�c
����1�����c���⺬����̖��һԪһ�η��̵Ľⷨ��
����2���y�c����̖ǰ����̖ؓ�r��ȥ��̖�r��ӛ׃̖��
�����̌W�^��
����һ�������ᆖ
����1�������з��̣�
������1��5x��2=8��2��5+2x=4x
����2��ȥ��̖���t��ʲô������헡�Ҫע��ʲô��
������������
����һԪһ�η��̵ĸ��
������44x+64=3283+x=��45+x��y��5=2y+1����������ʲô��ͬ������
����ֻ����һ��δ֪�������Һ���δ֪����`ʽ�Ӷ�����ʽ��δ֪���ĴΔ���1���@�ӵķ��̽���һԪһ�η��̡�
������1���Д�������Щ��һԪһ�η���
����x=3x��2x��=��1
����5x2��3x+1=02x+y=1��3y=5
������2���ⷽ�̣�1����2��x��1��=4
������2��3��x��2��+1=x����2x��1��
�������{ȥ��̖�r����̖����քe������̖�ȵ�ÿһ헣�����̖ǰ���ǡ�����̖��ע��ȥ����̖��Ҫ��׃��̖�ȵ�ÿһ헵ķ�̖��
�����a�䣺�ⷽ��3x��[3��x+1������1+4��]=1
�����f�����������ж�����̖�r��һ�㑪����ȥС��̖����ȥ����̖�����ȥ����̖�ķ���ȥ��̖��ÿȥһ����̖�ϲ�ͬ��һ�Σ��Ժ����\�㡣
��������얹̾���
�����̿ƕ���9퓣�������1��2��3��
�����ġ�С�Y
�����W����һԪһ�η��̵ĸ��������̖��һԪһ�η��̵Ľⷨ���÷�����ȥ��̖�r����Ҫ©����̖�е�헣����Ҳ�Ҫ���e��̖��
�����塢���I
����1���̿ƕ���12����}6��
����2����1�}��
�������꼉�σԔ��W�̰� 11
�����̌WĿ�ˣ�
����1�����_���┵�S�����x�����┵�S����Ҫ�ء�
����2���������픵�ڔ��S�ϵı�ʾ�����Լ����Ô��S���^���픵�Ĵ�С��
����3�������෴�������x����
����4�����W���B���νY�ϵ�˼�뷽�������B�W�����^�졢�w�{�c������������
�������c�y�c��
����1�����_���Ք��S�Į������Ô��S�ϵ��c��ʾ���픵������֪�����෴����
����2�����픵�͔��S�ϵĵ��c�Č����Pϵ��
�����̌W������
��������̽������
�����W��ָ����
�����^��w�{����
�����̌W�^����
����һ���龰���룺
������1������x�ض�Ӌ�����n��43���������x�ض�Ӌ�Ć��}��
������2���҂��ܷ�����Ɯض�Ӌ�ĈD�α�ʾ���픵�أ�
���������v�����n���J����x�n����43���45퓣�������І��}
������1����һ�lˮƽֱ������ֱ����ȡһ�cO�������x�x�x�����xȡijһ�L������x�x�x�x��Ҏ�����ҵķ����x�x�x���͵õ��˔��S��
�������ǣ�+3�����Ô��S��λ��ԭ�c��߅3����λ���c��ʾ����4�����Ô��S��λ��ԭ�c��߅4����λ���c��ʾ���ڔ��S��λ��ԭ�c��߅�c��ʾ���ڔ��S��λ��ԭ�c��߅1��5���c��ʾ���κ����픵�������Ô��S�ϵ�һ���c����ʾ��
�����������}�v�⡢얹����
������1����D��ָ�����S��A��B��C��D���c��ʾʲô����
����ADCB
�����C2�C10123
�����⣺�cA��ʾ��2���cB��ʾ2���cC��ʾ0��
�����cD��ʾ��1
�����������������S���Ô��S�ϵ��c��ʾ���Ђ�����
������5��0��5����4������
�����ġ��^�m̽��
����2�c��2��ʲô��ͬ�c�c��ͬ�c�������ڔ��S�ϵ�λ����ʲô�Pϵ��5�c��5���c�C�أ�
��������ɂ���ֻ�з�̖��ͬ����ô�҂��Q����һ��������һ�������෴����Ҳ�Q�@�ɂ��������෴�����e��0���෴����0��
�����ڔ��S�ϣ���ʾ�����෴���ăɂ��c��λ��ԭ�c�ăɂȣ������cԭ�c�ľ��x��ȡ�
����������1��5���෴���Ǩx�x���x�x���෴���ǡ�3��5��
�����hһ�h
�������S�ϵăɂ��c����߅�c��ʾ�Ĕ��c��߅�c��ʾ�Ĕ������ӵ�.��С�Pϵ��
�������S�ϱ�ʾ�Ĕ����x�x�x߅�Ŀ��Ȩx�x�x߅�Ĵ������x�x�x0��ؓ���x�x�x0�������x�x�xؓ����
�������������^������3�x5��0�x��4����3�x��2��5��
����3����������
������1��ʲô�ǔ��S�����Ӯ����S��
������2�����픵�c���S�ϵ��c֮�g�������ӵ��Pϵ��
������3��ʲô���෴����������һ�������෴����
������4��������Ô��S���^���픵�Ĵ�С��
����5���S�þ�����
������1�������f�����_���ǣ���
����A�����S�ϵ��cֻ�ܱ�ʾ���픵
����B��һ����ֻ���Ô��S�ϵ�һ���c��ʾ
����C����1��3֮�gֻ��2
����D���ڔ��S���xԭ�c2����λ�L�ȵ��c��ʾ�Ĕ���2
������2���Z�䣺�١�5���෴�����ڡ�5�c+3�����෴���ۡ�5��5���෴���ܡ�5��5�����෴����0���෴����0�ޡ�0=0�������f�������_���ǣ���
����A���٢ڢ�B���ڢۢ�C���٢�D���ۢܢݢ�
������3�����ڡ�4��С��4�������Шx�x�x�x�x�x��
������4���á���������̖���
�����١�5�x�x��7��0�x�x��2��0��01�x�x�x��0��1
������5���������и������෴��
����3��4����3��0��a��2a��3��
�������꼉�σԔ��W�̰� 12
����һ�����|����Ŀ��
������һ��֪�R�̌W�c
����1�����յ���Ҫ�أ������_������
����2���܌���֪�����ϱ�ʾ���������f������֪�c����ʾ�Ĕ���
��������������Ӗ���c
����1��ʹ�W���ܵ��ь��H���}����ɔ��W���}��Ӗ�������γɑ��Ô��W�����R��
����2�����W���B���νY�ϵ�˼�뷽����
���������������B�c
����ʹ�W�������˽┵�W��Դ�ڌ��`�����^���ַ����ڌ��`���q�CΨ�����x�^�c��
�������ģ������B�c
����ͨ�^�����o�W���ԈD�����Ľ�����ͬ�r���ڔ��εĽY�ϣ��W�����õ����C�������ܡ�
���������W������
����1���̌W�����������̎����������W�������w��ԭ�t��ʼ�K؞�������l��Ȥ�����X���á����l�T���������C�����Ľ̌W������
����2���W���W�������֮������X��������Ҫ�أ����֡����X��������
�����������c���y�c�����c����Q�k��
����1�����c�����_���ծ��������ϵ��c��ʾ���픵��
����2���y�c�����픵���ϵ��c�Č����Pϵ��
�����ġ��n�r����
����1�n�r
�����塢�̾ߌW�ߜʂ�
������X��ͶӰ�x�������zƬ��
���������������ӻ���OӋ
��������ͬ�������W��������Ҫ�أ�����ʾͶӰ�������ք��X����
�����ߡ��̌W���E
������һ�����O�龳���������n
�����������֪�R�ض�Ӌ����;��ʲô��
���������ض�Ӌ���Ԝy���ض�
��������ʾͶӰ1��
���������ض�Ӌ������һ���ض�Ӌ��Һ����0��20���̶ȣ�һ���ض�Ӌ��Һ����0��5���̶ȣ�һ���ض�Ӌ��Һ����0�̶ȡ�
�������������ض�Ӌ����ʾ�Ĝض��Ƕ��٣�
��������2�棬��5�棬0�档
�����҂��ܷ�����Ɯض�Ӌ�ĈD�α�ʾ���픵�أ�
�����@�N��ʾ���ĈD�ξ��ǽ����҂�Ҫ�W�ă��ݡ�������n�}����
�������̷��f�����Ĝض�Ӌ�Ø����x���Ŀ̶ȁ���ʾ�ضȵĸߵ��@�������l�����������n��Ҫ�W�ă��ݡ����ُĜض�Ӌ�@�����������������о����ȼ��l�ˌW���ČW���dȤ����ʹ�W���ܵ��ь��H���}����ɔ��W���}��Ӗ�������B���Ô��W�����R��
����������̽����֪���v�����n
����1���Į���
�����c�ض�Ӌ��ƣ�������һ�lֱ���Ϯ����̶ȣ������x������ֱ���ϵ��c��ʾ������ؓ�����㣬���w�������£�
������һ������ֱ����ԭ�cԭ�c��ʾ0���ஔ�ڜض�Ӌ�ϵ�0�棩��
�����ڶ�����Ҏ����ԭ�c���ҵĞ���������ô�෴�ķ���ԭ�c���t��ؓ�����ஔ�ڜض�Ӌ�ϡ����Ϟ�����0������ؓ����
�������������x���m�����L�Ȟ��λ�L�ȣ��ஔ�ڜض�Ӌ��ÿ1��ռ1С����L�ȣ���
�������̷��f�����̎�߅�v��߅ʾ�����W������һ�𮋈D�����B�W�����֡����X�͌��H����������ͬ�r���������һ�N��Ҫ����؞���ڸ����γ��^�̵�ʼ�K���W�����J֪�^�����I���@�N˼�뷽����
�����W���^�쮋�õ�ֱ����˼�������}��
��������ʾͶӰ1��
������1��ԭ�c��ʾʲô����
������2��ԭ�c�ҷ���ʾʲô����ԭ�c��ʾʲô����
������3����ʾ+2���c��ʲôλ�ã���ʾ��1���c��ʲôλ�ã�
������4��ԭ�c����0.5����λ�L�ȵ�A�c��ʾʲô����ԭ�c����λ�L�ȵ�B�c��ʾʲô����
���������ώ����D�IJ��E���W��˼����һ�lˮƽ��ֱ���϶�����ʲô��Ȼ��w�{���Ķ��x��
�����W����ӣ�ͬ�W��˼������Ҫ��ͬ�������������m���a�䣬�Z��ͨ혺��e�ֻش𡣴��˼���ʂ�������a�䡣
�������̷��f����ͨ�^���^�졪ȡ�˼�������������_��չ�F֪�R���γ��Ǐĸ����J�R�����������J�R���^�̣��W���ګ@ȡ֪�R���^���У��I�����W˼���˼�S�������������R��Ӗ���W���w�{�����Ϳ��^���_������
�����̎������W���ش�o��϶�����m��������
����2���Ķ��x��Ҏ����ԭ�c��������͆�λ�L�ȵ�ֱ��������
������W��������}���Ϟ�ʲôҪҎ��ԭ�c��������͆�λ�L���أ���������ʲô���ã������W���Y�Ϝض�ӆ���_�ش��@�����}���Ķ�֪����Ҫ�ص���Ҫ�ԣ��˽�����ȱһ���ɣ��J�R�������Д�һ�lֱ���Dz��ǵ�������
�����W����ӣ�ͬ��֮�g��ǰ����֮�gӑՓ��ʹ�W����ֱ�^�J�R�����������J�R��
����3���Lԇ������얹̾���
����Ո��һش����І��}��
��������ʾͶӰ2��
������1�������fһ�lֱ����һ�l������������ʲô��
������2���������������������������ָ���e�����
�����W����ӣ��W��˼��������ӑՓ����ú��e�ֻش�
���������W������ش��M���u�У����_���Ɇ����}Ŀ���̎��o���v�⡣
�������̷��f�����˽M������Ŀ����얹̵ĸ��
�����𰸣���2����ȱԭ�c����ȱ�����۲����侀����ֱ������ȱ��λ�L�ȣ������ьW��ע����ͬһ��݆�ϱ����ͬһ��λ�L���M�ж������ݢ��ǣ�ͬ�r�ߞ�W��ƽ��ֱ������ϵ����A��
����4�����픵�c���c���Pϵ
����ͨ�^���ŵČW���҂�֪�����е����픵���������ϵ��c����ʾ��
������1��һ�l����������ʾ���и������c��
����1��5��0����2.5��
�����W��������ͬ�W���ھ������Ϯ�һ�l��Ȼ�����Ϙ˳����c��һ���W�����ݡ��̎�Ѳ��ָ�����l�F���}���r�m����
�������̷��f�����W�������Լ��������������B�W�����H������������1�ǰѽo�������픵���ϵ��c����ʾ������ɡ����������Ρ���˼�S�^�̣������ڌW�������������⡣
��������ʾͶӰ4��
������2ָ����A��B��C��D��E���c�քe��ʾʲô����
�������W��˼��һ����Ȼ��W���e�ֻش�
�����⣺A��ʾ��3��B��ʾ��C��ʾ3��D��ʾ��E����
�������̷��f������2���W���f���ϵ��c��ʾ�����픵��������ɡ��Ρ�����������˼�S�^�̡���1����2�ĸ��Բ�ͬ�ăɂ����棬�w�F�����νY�ϣ��B�˔���֮�g��D���Ĕ��W˼�롣
����5���Lԇ������얹̾���
��������ʾͶӰ5��
�������f��������A��B��C��D��O��M���c��ʾʲô����
�����ڌ���3��1.5����6��2.25����5��1
�����������ϵ��c��ʾ������
�������̷��f�������}���c�x�����������}�ɔ����c�������Mһ��얹̼�������W�ă��ݡ�
�����������w�{�Y
�����������Ƿdz���Ҫ�Ĕ��W���ߣ���ʹ����ֱ���ϵ��c�����ˌ����Pϵ������ʾ���c��֮�g�ă���ϵ���ǎ����W�����┵�W���W�����W����Ҫ˼�뷽�����������픵�����P���|���\�㶼�ǽY���M�е�
������������Ҫ�أ����_�خ���������ͬ�W�������е����픵�������ϵĸ��c����ʾ�����Ƿ��^�������������ϵĸ��c�������Ƕ���ʾ���픵���Ժ����о���
�����ˡ��S�þ���
����1�����}
������1��ֱ�����ǣ���
������2����ֱ������
������3���κ�һ�����픵���������ϵ��c����ʾ����
������4���ϵ�ԭ�c���x����3���c����ʾ�Ĕ���+3����
������5����ԭ�c��߅��ʾ�Ĕ���ؓ������߅��ʾ�Ĕ���������ԭ�c��ʾ�Ĕ���0������
����2����һ�l��݆����������ʾ���и������c����5��0��+3.2����1.4
�����š��������I
���������������}���n����56�1��2��
�����������x���}���n����56퓼���57�B�M1��
����������˼���}��
�������ڔ�݆�Ͼ�ԭ�c3����λ�L�ȵ��c��ʾ�Ĕ���_____________
�������ڔ�݆�ϱ�ʾ��6��`�c��ԭ�c��___________�ȣ����xԭ�c___________����λ�L�ȣ���ʾ+6���c��ԭ�c��__________�ȣ����xԭ�c____________����λ�L�ȡ�
�������̷��f�������ڌW����֪�R�����ܡ���������lչ���M��ͬ�����ԷӴεز������I����W�������y�͌W�������ČW����ʹ���������_����V��Ҏ���Ļ���Ҫ��ʹ���W���ܰlչ�����Ĕ��W���ܡ�
����ʮ������OӋ
�����S�þ�����
����1�����̡̡���2����
�������I��
������һ�������}
����1����1��������
������2��������
����2��������
�����������x���}��
����3����B�M1����1����6����2����1����3��3����4��0
����������˼���}���٢���6���ң�6
����̽�����
������1�����ϱ�ʾ�����xԭ�c3����λ�L�Ⱥ�4.5����λ�L�ȵ��c�����á�<��̖���@Щ�c����ʾ�Ĕ�����������
������2�������ȡ�4������2������������
�������������r������Ҫ�أ�ԭ�c��������λ�L��ȱһ���ɡ�
������1�����ϣ����xԭ�c3����λ�L�Ⱥ�4.5����λ�L�ȵ��c���Ѓɂ��������քe��ԭ�c�������P��ԭ�c���Q�������@Щ�c���@Щ�c����ʾ�Ĕ��Ĵ�С�����г����ˣ�
������2�����Ϯ������ڡ�4��������2�Ĕ��ķ������@�������������c����ʾ��������������������2������˼��С�ڻ����2��
�����⣺��1���ϣ����xԭ�c3����λ���c��+3�͡�3�����xԭ�c4.5����λ���c��+4.5�͡�4.5��
�����ɈD��������4.5<��3<3<4.5
������2�����Ϯ������ڡ�4��������2�Ĕ��ķ�����
�����ɈD֪�����ڡ�4��������2�������ǣ���3����2����1��0��1��2��
�����c�u�����ã����νY�ϣ��ǽ��@һ��}�ĺ÷�����
�������꼉�σԔ��W�̰� 13
�����̌WĿ��
����1��֪�R���J�R���εĿ��g���������A�����A�F����ȣ��������е���֮ͬ̎�Ͳ�֮ͬ̎��
����2��������ͨ�^���^���W���^�����w�g���������w�����w�g��ϵ�ͅ^�e�����ܸ������w�������������M�к��η��
����3����У������R�������W���e�O���c�����W����^���У����B�c���˺���������������
�����̌W���c��
�����J�RһЩ�����Ď��w�����������@Щ���w��������
�����̌W�y�c��
�����������w�������������w�M��
�����̌W�^�̣�
����һ���O����̽
�������O�龰���������n
������С�W�ĕr��W������Щƽ��D�κ͎ΈD�Σ���������߀Ҋ����Щ���w?
�����W���O��
�����W���Լ���˼�����ᆖ
�����̎���������ʾ��̽�}Ŀ
���������Ҋ�Ď��w����Щ?
�������@Щ���w��ʲô����
�����ۈA���w�c�����w��ʲô��.��֮ͬ̎�Ͳ�֮ͬ̎
�����܈A���w�c�A�F�w��ʲô����֮ͬ̎�Ͳ�֮ͬ̎
�����������ķ��
�����ގ��w�ķ��
�����W����̽(���к������ԌW����ָ��)
�����e���f�f�����е����w��Щ��ƈA�����A�F�������w���L���w�����������w?
�����f�f�����ą^�e
�����������ɺ�̽
����1��ᘌ��A�����A�F�������w���L���w�����������w�������J�R���ص��M����̽
����2�����@Щ��ƈA�����A�F�������w���L���w�����������w�ķ��
�������ԭ�t���W�����ش��е����a�䡢�������u�r���̎����I�c���������Y��
���������|����̽��
�����f�f��߀��ʲô�ɻ���}(�ɌW�����ώ������������Ć��})
�����ġ��\����չ��
���������W���Ծ����}��
����Ո�Y�ϱ������W��֪�R�e���f������λ����Ď��w�����f�f������
�����̎���ʾ�\����չ�}��
����(Ҫ�����̲ă��ݱM����Ҫԇ�}���ȫ�����д�����)
�����n���Y
�������I����
�����塢�̺�˼
�������꼉�σԔ��W�̰� 14
����һ���̌WĿ��
����1�����˽��෴���x���Ļ��A�ϣ�ʹ�W���˽���ؓ���ĸ���͌W����ؓ�������x��
����2��ʹ�W�������_�Д�һ����������߀��ؓ�������_��Ȳ�������Ҳ����ؓ����
����3���W������ؓ����ʾ���H���}�о����෴���x������
���������̌W���c���y�c
�������c����ؓ���ĸ���
�����y�c��ؓ���ĸ���
���������̾�
����ͶӰƬ������ͶӰ�x
�����ġ��̌W����
����(һ)����
���������҂�֪�������˱�ʾ���w�Ă������������a����1��2��3��4�����@Щ�����҂���������ʲô��?
����������Ȼ��
�����������˱�ʾ���]�С�����������һ��ʲô��?
����������Ȼ��0
�����������y����Ӌ��ĽY�����������r�������M��ʲô��?
���������֔�(С��)
����������Ҋ���ĸ������S�����a���������Ҫ������lչ�ġ�Ոͬ�W����һ�룬�ڬF���������Ƿ�߀�������e��͵Ĕ���?��������������̎���ں�ƽ��155�ף�������߷������ʬ��߳���ƽ��8848.13�ף�����ij����ߚ��������8�z�϶ȡ�
����Ո�W���Ô���ʾ�@Щ����������ʾ���y��
�������������ܱ�ʾ�@Щ�����҂���Ҫ����һ�N���@���DZ����n��Ҫ�W���ă��ݡ�[�����1��1�����cؓ��]
����(��)���n�̌W
����1���෴���x����
���������ڬF�������У��҂���������һЩ�����෴���x���������磺(ͶӰƬ�@ʾ)
����(1)��܇��|���2.5ǧ���������1.5ǧ��;
����(2)��؏�����6�z�϶��½�������6�z�϶�;
����(3)�L�~����10���½�5�ס�
���������W�����_�����෴���x������������(1)�Ѓɂ���(2)���෴�����x
����Ո�W���e��һЩ�෴���x�����Č�����
�����̎��w�Y���෴���x�е�һЩ�����~�У�ӯ���c̝�p�������c֧���������c�p�٣��\�M�c�\���������c�½��ȡ�
����2�������cؓ��
����������С�W��W�^�Ĕ��ܱ�ʾ�@Щ�����෴���x������?�����ʾ�����෴���x������?
�����Ɏ���ӑՓ��ó����҂���һ�N���x����Ҏ�������ģ��á�+��(�x����)̖����ʾ��ͬ�r����һ�N�c���෴���x����Ҏ����ؓ�ģ��á�-��(�x��ؓ)̖����ʾ��
�����������磬�������6��ӛ��+6��(�x����6�z�϶�)����ô����6��ӛ��-6��(�x��ؓ6�z�϶�)��Ոͬ�W����ͬ�ӵķ�����ʾ(1)��(2)���}��
��������(1)�����|���2.5ǧ��ӛ��+2.5ǧ��(�x����2.5ǧ��)����ô�������1.5ǧ��ӛ��-1.5ǧ��(�x��ؓ1.5ǧ��);(2)�������10��ӛ��+10��(�x����10��)����ô�½�5��ӛ��-5��(�x��ؓ5��)��
����������+6��+10��+2.5��ǰ����С�+��̖�Ĕ�������������-6��-5��-1.5��ǰ����С�-��̖�Ĕ�����ؓ������̖����ʡ�Բ�������+5���Ԍ���5����ؓ����̖ؓ��ʡ�Բ�����?
��������(ӑՓ��ó�)���ܡ�
��������(�Ԝض�Ӌ����)�ض�Ӌ�е�0���DZ�ʾ�]�Мضȣ���ͨ����ʾˮ�Y�ɱ��r�Ĝضȣ������Ϝض��c���ضȵ�.�ֽ��c����˵ó�����Ȳ�������Ҳ����ؓ����
����(��)������
����1���W������n����4퓾���1��2��3
����2���a�侚��
����(1)��-2��+2.5��0��-0.35��11�У������ǣ�ؓ����;
����(2)�����|��������ô��-50�ױ�ʾʲô��˼?������Ϟ�������ô��-50���ֱ�ʾʲô��˼?
����(3)�W�����Ե���һ��ӛ��0����ô1�ǡ�2�ǡ�3�ǡ����ͱ�ʾ��0��1��2������ô���µڶ��ӱ�ʾ�顣
����(��)�Y
����1������ؓ�����Ժ����ı�ʾ�෴���x�����������෴���x�������������һ�N����������ʾ����ô��һ�N��������ؓ����ʾ��
����2���ڱ�ʾ�����෴���x�����r������һ�N���x����Ҏ���������ɸ������H��r�Q����
����3��Ҫ�eע����Ȳ�������Ҳ����ؓ����������ؓ����������]һ�����r��һ��Ҫ���]���ķ�̖���@�cС�W��W�^�Ĕ��кܴ�ą^�e��
����(��)���I
����Ҋ���I1.1�����I��
�������꼉�σԔ��W�̰� 15
�����̌WĿ�ˣ�
����1���˽�ƽ�Ƶĸ�����M���c��ƽ�ƣ�����ƽ�Ƶ����|���ܽ�Q���ε�ƽ�Ɔ��}
����2�����B�W���Ŀ��g�^��W�����\�ӵ��^�c�������}��
�������c��ƽ�Ƶĸ�������D������
�����y�c��ƽ�Ƶ����D��
�����̌W�^��
����һ���^��D���γ�ӡ��
�������������S�������ĈD����������������ͬ�����c��Ոͬ�W�����p����D����
�����^������D�Σ��҂��l�F��������һ���ֲ������������؏ͣ�����o��һ���ֲ���������������W��˼��ӑՓ�������e���f����
�������������֪���`̽��
����ƽ�ƣ�
������1����һ���D�����w��ijһ�����Ƅӣ����õ�һ���µĈD�Σ��D���cԭ�D�ε��Π�ʹ�С��ȫ��ͬ��
������2���D���е�ÿһ�c��������ԭ�D���е�ijһ���c�ƄӺ�õ��ģ��@�ɂ��c�nj����c��
������3���B�Ӹ��M�����ľ���ƽ������ȡ��D�ε��@�N׃�Q������ƽ��׃�Q�����Qƽ��
����̽�����OӋһ�����εĈD��������һ�������ļ��������棬�L��һ���Π��С��ȫһ�ӵĈD��
���������W����Ҏ�ɣ��l�Fƽ������
�����������������얹�
��������D��(1)ƽ��������ABC��ʹ�cA�\�ӵ�A`������ƽ�ƺ�Ħ�ABC
�������^��̽ӑ����ͨ�^�c��ƽ�ƣ����ε�ƽ�ƿ��YҎ�ɣ��o�����x
����̽����ӿ���ʹ�W�����Mһ���˽�ƽ��
�����ġ�얹̾���
�����n��33퓣�1��2��4��5��6��7
�����塢С�Y
������ƽ���^���У������c���B��`����Ҳ������һ�lֱ���ϣ����D��ƽ�Ƶķ���������һ߅����ֱ���ķ���r����ô��߅�ϵČ����c�����@�lֱ���ϡ�2����ƽ�Ƶ���������ƽ�о�����������Pϵ�ǽ�7�}���õķ�����
�����������I
�����n��P30����}5.4��3�}
�����꼉�σԔ��W�̰������P���£�
���꼉�σԔ��W�̰�01-19
���꼉�σԔ��W�̰�����Ʒ��10-21
��̰����꼉�σԔ��W�̰�01-16
������꼉�σԔ��W�̰�02-25
���꼉�σԔ��W�̰��˽̰�11-05
(���x)���꼉�σԔ��W�̰�07-03
���꼉�σԔ��W�̰����08-27