���꼉(j��)��(sh��)�W(xu��)�̰�ģ��R��7ƪ
�����ڽ̌W(xu��)�������_(k��i)չ�̌W(xu��)���(d��ng)ǰ���r(sh��)����Ҫ�����̰��������̰�������߽̌W(xu��)�|(zh��)�����յ��A(y��)�ڵĽ̌W(xu��)Ч�����̰�Ҫ��ô���أ�������С���ʹ�������İ��꼉(j��)��(sh��)�W(xu��)�̰�7ƪ��ϣ���܉��������ҡ�
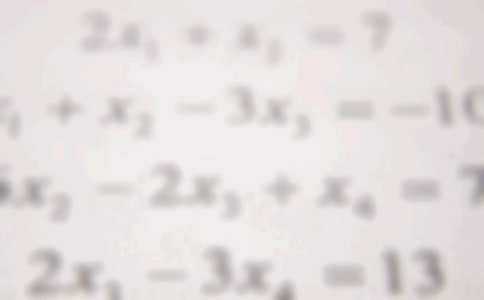
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ1
�����̌W(xu��)Ŀ��(bi��o)
����֪�R(sh��)�c����
�����ö�Ԫһ�η��̽M��Q��Ȥ��(ch��ng)���еĔ�(sh��)�ֆ�(w��n) �}���г̆�(w��n)�}���w�{�÷���(�M)��Q��(sh��)�H��(w��n)�}��һ�㲽�E.
�����^(gu��)���c����
����1.ͨ�^(gu��)�O(sh��)�Æ�(w��n)�}�����W(xu��)���w��(hu��)������(f��)�s��(w��n)�}��˼������.
����2.�W(xu��)���M(j��n)һ����(j��ng)�v���w�(y��n)�з��̽M��Q��(sh��)�H��(w��n)�}���^(gu��)�̣��w��(hu��)���̽M�ǿ̮��F(xi��n)��(sh��)���� ����Ч��(sh��)�W(xu��)ģ��.
������БB(t��i)���c�r(ji��)ֵ�^
�����ڌW(xu��)��(x��)�^(gu��)�����W(xu��)���w�(y��n)�я�(f��)�s��(w��n)�}���麆(ji��n)�Ά�(w��n)�}�IJ��ԣ��w�(y��n)�ɹ��У�ͬ�r(sh��)���B(y��ng)�W(xu��)���˷����y����־���⣬ ��(sh��)�������ģ����Ą�(l��)�W(xu��)������ ���������B(y��ng)�W(xu��)���ĈF(tu��n)�(du��)����.
�����̌W(xu��)���c(di��n)
����1.�����w��(hu��)�з��̽M��Q��(sh��)�H��(w��n)�}��`���E.
����2.�W(xu��)��(hu��)�ÈD�� �����^��(f��)�s�Ĕ�(sh��)���P(gu��n)ϵ��(w��n)�}��
�����̌W(xu��)�y�c(di��n)
��������(sh��)�H��(w��n)�}�D(zhu��n)�� �ɶ�Ԫһ�η��̽M�Ĕ�(sh��)�W(xu��)ģ��;��(hu��)�ÈD��������(sh��) ���P(gu��n)ϵ��
�����̌W(xu��)��(zh��n)�䣺
�����̾ߣ��̲ģ��n������X(ҕ�l������)
�����W(xu��)�ߣ��̲ģ�����(x��)��
�����̌W(xu��)�^(gu��)��
������һ�h(hu��n)��(ji��)����(f��)��(x��)�ᆖ(w��n)(5��犣��W(xu��)���ڴ�)
������(n��i)�ݣ���գ�
����(1)һ��(g��)��λ��(sh��)����(g��)λ��(sh��)���� ��ʮλ��(sh��)���� ���t�@��(g��)��λ��(sh��)�ô���(sh��)ʽ��ʾ�� ;�����Q��(g��)λ��ʮλ�ϵĔ�(sh��)�ֵõ�һ��(g��)�µă�λ��(sh��)���ô���(sh��)ʽ��ʾ�� .
����(2)һ��(g��)��λ��(sh��)����(g��)λ�ϵĔ�(sh��)�� ��ʮλ�ϵĔ�(sh��)�� �����������֮�g����һ��(g��)0���͵õ�һ��(g��)��λ��(sh��)���@��(g��)��λ��(sh��)�ô���(sh��)ʽ���Ա�ʾ�� .
����(3)�Ѓɂ�(g��)��λ��(sh��) �� ������� ���� ����߅���͵õ�һ��(g��)��λ��(sh��)����ô�@��(g��)��λ��(sh��)�ô���(sh��)ʽ��ʾ�� ;����� ���� ����߅�����õ�һ��(g��)�µ���λ��(sh��)����ô�@��(g��)��λ��(sh��)�ô���(sh��)ʽ�ɱ�ʾ�� .
�����ڶ��h(hu��n)��(ji��)���龳����(10��犣��W(xu��)����(d��ng)�X˼����ȫ�ཻ��)
������(n��i)�ݣ�С���ְ��T��Ħ��܇����С���ڹ�·�τ������D��С��ÿ��1С�r(sh��)�����������r.���� �_��С����12:00�r(sh��)��������̱��ϵĔ�(sh��)��?
���������h(hu��n)��(ji��)�������W(xu��)��(x��)(10��犣�С�MӑՓ���ҵ����P(gu��n)ϵ����Q ��(w��n)�})
������(n��i)�ݣ���1
�����ɂ�(g��)��λ��(sh��)�ĺ���68�����^��ă�λ��(sh��)����߅�������^С�ă�λ��(sh��)���õ�һ��(g��)��λ��(sh��);���^��ă�λ��(sh��)����߅�����^С�ă�λ��(sh��)��Ҳ�õ�һ��(g��)��λ��(sh��).��֪ǰһ��(g��)��λ��(sh��)�Ⱥ�һ��(g��)��λ��(sh��)��2178�����@�ɂ�(g��)��λ��(sh��).
�����W(xu��)���Ȫ�(d��)��˼����1���ڴ˻��A(ch��)�ϣ��̎�����(j��)�W(xu��)��˼����r�M�������cӑՓ.
�������ĭh(hu��n)��(ji��)��얹̾���(x��)(10��犣��W(xu��)���Lԇ��(d��)����Q��(w��n)�}��ȫ�ཻ��)
������(n��i)�ݣ�����(x��)
����1.һ��(g��)��λ��(sh��)���pȥ���ĸ�λ��(sh��)��֮�͵�3�����Y(ji��)����23;�@��(g��)��λ��(sh��)�������ĸ�λ��(sh��)�� ֮�ͣ�����5������(sh��)��1.�@��(g��)��λ��(sh��)�Ƕ���?
����2.һ��(g��)��λ��(sh��)����һ��(g��)��λ��(sh��)��3����������@��(g��)��λ��(sh��)������һ��(g��)��λ��(sh��)���� ߅�c������߅���õĔ�(sh��)֮�͞�8484.���@��(g��)��λ��(sh��).
��������h(hu��n)��(ji��)���n��С�Y(ji��)(5��犣��̎�����(d��o)�W(xu��)�����Y(ji��)һ�㲽�E)
������(n��i)�ݣ�
����1.�̎��ᆖ(w��n)������(ji��)�n�҂��W(xu��)��(x��)����Щ��(n��i)�ݣ���(du��)�@Щ��(n��i)������ʲô�w��(hu��)���뷨?Ո(q��ng)�cͬ�齻��.
����2.�������ཻ�����Y(ji��)���з���(�M)��Q��(sh��)�H��(w��n)�}��һ�㲽�E.
������ ���h(hu��n)��(ji��)���������I(y��)
������(n��i)�ݣ���(x��)�}7.6
����A�M(��(y��u)����) 2��3��4
����B�M(���)2��3
����C�M(������֮һ��)2
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ2
����֪�R(sh��)�Y(ji��)��(g��u)��
�������c(di��n)�c�y�c(di��n)������
��������(ji��)��(n��i)�ݵ����c(di��n)�ǵ��������ε��ж�����.���������C���ɗl������ȵ���Ҫ���������ǰ��������нǵ�����P(gu��n)ϵ�D(zhu��n)����߅������P(gu��n)ϵ����Ҫ����(j��)���˶�����C����������ṩ����һ�N�������@�DZ���(ji��)�����c(di��n).��Փ1��2�ṩ�C����߅�����εķ�������Փ3��ֱ�������ε�һ�l��Ҫ���|(zh��)����ֱ������������߅�ͽǵĵ����P(gu��n)ϵ��(j��ng)���õ�����Փ.
��������(ji��)��(n��i)�ݵ��y�c(di��n)�����|(zh��)�c�ж��ą^(q��)�e�����������ε����|(zh��)�������ж������ǻ��涨�����}�O(sh��)�c�Y(ji��)Փ�����෴.�W(xu��)���ڑ�(y��ng)�������ĕr(sh��)��(j��ng)�������������W(xu��)���J(r��n)�R(sh��)�ж��c���|(zh��)�ą^(q��)�e���@�DZ���(ji��)���y�c(di��n).���Ȿ��(ji��)������?j��n)����}Ҳ���y�c(di��n)֮һ�����Ϲ�(ji��)�Y(ji��)���W(xu��)�������ս��}��˼·����.����֪�R(sh��)�c(di��n)�����ӣ��}Ŀ�ď�(f��)�s�̶�Ҳ��ߣ�һ��Ҫ�W(xu��)���������ⶨ������Փ�������ڽ��}�r(sh��)�ėl���õ����Ă�(g��)�����������.
�����̷����h:
��������(ji��)�n�̌W(xu��)������Ҫ�ǡ��ԌW(xu��)�������w��ӑՓ̽���������ڔ�(sh��)�W(xu��)�̌W(xu��)��Ҫ�����^(gu��)����V�W(xu��)���F(xi��n)�ɽY(ji��)Փ���ᳫ�̎��Ą�(l��)�W(xu��)��ӑՓ��Q��(w��n)�}�ķ���������(d��o)����̽����(sh��)�W(xu��)�ă�(n��i)��Ҏ(gu��)�ɡ����w�f(shu��)�����£�
����(1)���c̽���l(f��)�F(xi��n)���I(l��ng)��֪�R(sh��)�γ��^(gu��)��
�����W(xu��)���W(xu��)��(x��)�^(gu��)�������}�ͻ��涨���ĸ�����������(w��n)�}���������������|(zh��)�����������}��ʲô?��һ���W(xu��)���������ˣ�����(l��i)��(w��n)�������}�Ƿ������?��ͬ�W(xu��)���C�����ˣ���һ���W(xu��)�������l(f��)��.�����һ���W(xu��)�������ֿ��������ă�(n��i)�ݡ��@�Ӻ���Ȼ�͵õ��˵��������ε��ж�����.�@���W(xu��)���H�Ԅ�(d��ng)��(sh��)�`���e�O���c�l(f��)�F(xi��n)���M��M���ˌW(xu��)�����J(r��n)�R(sh��)�_ͻ��ʹ�W(xu��)���˷�˼�S��̽��Ķ��ԣ��@��呟��C(j��)��(hu��)����(du��)�����Įa(ch��n)���^(gu��)�̣������������I(l��ng)���(hu��)��
����(2)���á�ȡ��ČW(xu��)��(x��)�������@ȡ֪�R(sh��)��
���������|(zh��)�����ČW(xu��)��(x��)���҂��õ��ˎׂ�(g��)��Փ����Ȼ�뵽������(j��)���������ε��ж��������҂��ܵõ���Щ����ĽY(ji��)Փ�����f(shu��)��Щ��Փ��?�@�����W(xu��)���l(f��)����Ҋ(ji��n)��Ȼ���ҹ�ͬ����ӑՓ����һЩ�Ѓr(ji��)ֵ�ġ��������ǽ̲��е���Փ�������(l��i)������W(xu��)���ᵽ�IJ��������̎��������m��(d��ng)?sh��)��c(di��n)������(d��o)��
����(3)���Y(ji��)���γ�֪�R(sh��)�Y(ji��)��(g��u)
��������ʹ�W(xu��)����(du��)����(ji��)�n��һ��(g��)�������J(r��n)�R(sh��)�����ڽ��đ�(y��ng)�ã��̎��������(w��n)�}���W(xu��)��˼���ش�(1)�����ж�һ��(g��)�������ǵ���������?����Щ��������(j��)?(2)�����ж�һ��(g��)�������ǵ�߅������?
����һ.�̌W(xu��)Ŀ��(bi��o)��
����1.ʹ�W(xu��)�����յ��������ε��ж�����������Փ;
����2.���յ����������ж��������\(y��n)��;
����3.ͨ�^(gu��)���}�ČW(xu��)��(x��)����ߌW(xu��)����߉˼�S������������(w��n)�}��Q��(w��n)�}������;
����4.ͨ�^(gu��)�����W(xu��)��(x��)�İl(f��)չ�w�(y��n)�@ȡ��(sh��)�W(xu��)֪�R(sh��)�ĸ���;
����5.ͨ�^(gu��)֪�R(sh��)�Ŀv�M�w�Ƹ��ܔ�(sh��)�W(xu��)���q�C����.
������.�̌W(xu��)���c(di��n)�����������ε��ж�����
������.�̌W(xu��)�y�c(di��n)�����|(zh��)�c�ж��ą^(q��)�e
������.�̌W(xu��)�þߣ�ֱ�ߣ��C(j��)
������.�̌W(xu��)�������ԌW(xu��)�������w��ӑՓ̽����
������.�̌W(xu��)�^(gu��)�̣�
����1�����n����֪�R(sh��)��(f��)��(x��)
����(1)Ո(q��ng)ͬ�W(xu��)���f(shu��)���������}�ͻ��涨���ĸ���
������Ӌ(j��)�W(xu��)�������Լ����Z(y��)���f(shu��)�����@�����c(di��n)��(f��)��(x��)���ӷ����}�O(sh��)�ͽY(ji��)Փ��
����(2)���������ε����|(zh��)�����ă�(n��i)����ʲô?���z�(y��n)���������}�Ƿ�������}?
�������l(f��)�W(xu��)�����Լ����Z(y��)�Ԕ��������Y(ji��)Փ���̎��Լ�������o��Ҏ(gu��)��������
����1.���������ε��ж����������һ��(g��)�������Ѓɂ�(g��)����ȣ���ô�@�ɂ�(g��)������(du��)��߅Ҳ���.
����(��(ji��n)�Q���Ƚnj�(du��)��߅��).
�����ɌW(xu��)���f(shu��)����֪�����C��ʹ�W(xu��)���M(j��n)һ����Ϥ�����D(zhu��n)���锵(sh��)�W(xu��)�Z(y��)�Եķ���.
������֪����D����ABC�У���B=��C.
�������C��AB=AC.
�����̎�������(d��o)�W(xu��)��������
����(li��n)���C���P(gu��n)������ȵ�֪�R(sh��)֪�������蘋(g��u)����AB��AC�錦(du��)��(y��ng)߅��ȫ��������.��?y��n)���֪��B=��C���](m��i)�Ќ�(du��)��(y��ng)���߅�����������o������ɂ�(g��)�����εĹ���߅������o������(y��ng)��A�c(di��n)����.���W(xu��)����������������г������o�������W(xu��)�����ҳ�����BAC��ƽ�־�AD����BC߅�ϵ�`��AD���C������ȫ�ȵIJ�ͬ�������Ķ��Ƴ�AB=AC.
����ע�⣺(1)ҪŪ���ж������ėl���ͽY(ji��)Փ����Ҫ�c���|(zh��)��������.
����(2)�����f(shu��)��һ��(g��)�����ɵ���ȣ���ô����߅��ȡ�����?y��n)�߀δ�ж�����һ��(g��)����������.
����(3)�ж������õ��ĽY(ji��)Փ���������ǵ��������Σ����|(zh��)��������֪�������ǵ��������Σ��õ�߅߅�ͽǽ��P(gu��n)ϵ.
����2.��Փ1������(g��)�Ƕ���ȵ��������ǵ�߅������.
������Փ2����һ��(g��)�ǵ���60��ĵ����������ǵ�߅������.
����Ҫ�W(xu��)���Լ����C�@�ɗl��Փ.
����С�Y(ji��)���C���������ǵ��������εķ������ٵ��������ζ��x;�ڵ����������ж�����.
�����C���������ǵ�߅�����εķ������ٵ�߅�����ζ��x;����Փ1;����Փ2.
����3.��(y��ng)���e��
������1.���C�����������һ��(g��)��ǵ�ƽ�־�ƽ���������ε�һ߅����ô�@��(g��)�������ǵ���������.
��������:�W(xu��)�����D��������֪���C�����l(f��)�W(xu��)��������֪������Ǖr(sh��)���������]��(y��ng)����ǵăɂ�(g��)���Ԣ����c�����ă�(n��i)�ǻ��a(b��);���������c���������ăɂ�(g��)��(n��i)�ǵĺ�.Ҫ�CAB=AC�������C����B=��C����?y��n)���֪�?=��2�����Կ����O(sh��)���ҳ���B����C�c��1����2���P(gu��n)ϵ.
������֪����CAE�ǡ�ABC����ǣ���1=��2��AD��BC.
�������C��AB=AC.
�����C����(��)�ɌW(xu��)�����ݼ���.
�����a(b��)�����}��(ͶӰչʾ)
����1.��֪����D��AB=AD����B=��D.
�������C��CB=CD.
��������������w��(w��n)�}�r(sh��)Ҫͻ��߅���D(zhu��n)�Q�h(hu��n)��(ji��)��Ҫ�CCB=CD���蘋(g��u)��һ��(g��)�� CB��CD�����ĵ��������Σ��B�Y(ji��)BD�����C��CBD=��CDB������֪��B=��D����AB=AD���C��ABD=��ADB���Ķ��C�á�CDB=��CBD���Ƴ�CB=CD.
�����C�����B�Y(ji��)BD���� �У� (��֪)
����(��߅��(du��)�Ƚ�)
����(��֪)
������
����(�Ƚ̌�(du��)��߅)
����С�Y(ji��)�������һ��������������⣬�����m��(d��ng)?sh��)��o������(g��u)�������Σ��ҳ�߅���P(gu��n)ϵ.
����2.��֪���� �У� ��ƽ�־��c �����ƽ�־�����D���^(gu��)D��DE//BC��AC�cF����AB��E�����C��EF=BE-CF.
������������(du��)������(g��)�����g�P(gu��n)ϵ���M���D(zhu��n)��������P(gu��n)ϵ�����ڱ��}�Ѓɂ�(g��)��ƽ�־���ƽ�о�������ͨ�^(gu��)����߅���P(gu��n)ϵ��BE=DE,DF=CF�����C���Y(ji��)Փ.
�����C���� DE//BC(��֪)
������
����BE=DE,ͬ��DF=CF.
����EF=DE-DF
����EF=BE-CF
�����Y(ji��)��
����(1)�����������ж���������Փ.
����(2)���������κ͵�߅�����ε��C��.
������.����(x��)
�����̲� P.75��1��2��3.
������.���I(y��)
�����̲� P.83 �� 1.1)��2)��3);2��3��4��5.
������.����O(sh��)Ӌ(j��)
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ3
�����̌W(xu��)���h
����1��ƽ�о��ȷ־��ζ���
�������������һ�Mƽ�о���һ�lֱ���Ͻصõľ�����ȣ���ô��������ֱ���Ͻصõľ���Ҳ��ȡ�
����ע�����(xi��ng)�������е�ƽ�о��M��ָÿ�����ăɗl���x����ȵ������ƽ�о��M;���������l�����l���ϵ�ƽ�о��M�ɡ�
�������������ã������Á�(l��i)�C��ͬһֱ���ϵľ������;���Եȷ־��Ρ�
����2��ƽ�о��ȷ־��ζ�������Փ
������Փ1����(j��ng)�^(gu��)����һ�������c(di��n)�c��ƽ�е�ֱ������ƽ����һ����
������Փ2����(j��ng)�^(gu��)������һ߅�����c(di��n)�c��һ߅ƽ�е�ֱ������ƽ�ֵ���߅��
����ӛ�������������c(di��n)��+��ƽ�С��á����c(di��n)����
������Փ����;����1��ƽ����֪����;��2���C�����εı��֡�
�������y�c(di��n)����
��������(ji��)�����c(di��n)��ƽ�о��ȷ־��ζ�������?y��n)������H�����C�����Ρ�������λ�������Ļ��A(ch��)�������ǵ������С�ƽ�о��־��γɱ����������Ļ��A(ch��)��
��������(ji��)���y�c(di��n)Ҳ��ƽ�о��ȷ־��ζ��������ڌW(xu��)�����ν��|��ƽ�о��ȷ־��ζ��������J(r��n)�R(sh��)����������һ�����y�ȣ��ڼ���ƽ�о��ȷ־��ζ����ăɂ�(g��)��Փ�Լ����N׃ʽ���W(xu��)���y���(hu��)�Б�(y��ng)�Ӳ�Ͼ�ĸ��X(ju��)��������(hu��)�и��X(ju��)���r��Ȥ�����ղ������r�l(f��)�����̎��ڽ̌W(xu��)��Ҫ����ע�⡣
�����̷����h
����ƽ�о��ȷ־��ζ���������
�������������S��ƽ�о��ȷ־��ζ��������ӣ�����İ����ƽ�о��ȷ־��ζ���������ɏ�����ׂ�(g��)�Ƕȿ��]��
������?g��u)�����?sh��)�����룬��̶ȳߡ����I(y��)�����řڡ��ȵ�;
�����ڿ��Æ�(w��n)�}ʽ���룬�_(k��i)ʼ�r(sh��)�O(sh��)Ӌ(j��)һϵ���cƽ�о��ȷ־��ζ����������P(gu��n)�Ć�(w��n)�}�ɌW(xu��)���M(j��n)��˼�����о���Ȼ��o��ƽ�о��ȷ־��ζ�������Փ��
�����̌W(xu��)�O(sh��)Ӌ(j��)ʾ��
����һ���̌W(xu��)Ŀ��(bi��o)
����1��ʹ�W(xu��)������ƽ�о��ȷ־��ζ�������Փ��
����2���܉�����ƽ�о��ȷ־��ζ�������ȷ�һ�l��֪���Σ��M(j��n)һ�����B(y��ng)�W(xu��)�������D������
����3��ͨ�^(gu��)������׃ʽ�D�Σ��M(j��n)һ����ߌW(xu��)��������(w��n)�}�ͽ�Q��(w��n)�}��������
����4��ͨ�^(gu��)����(ji��)�W(xu��)��(x��)���w��(hu��)�D���Z(y��)�Ժͷ�̖(h��o)�Z(y��)�Եĺ��C��
���������̷��O(sh��)Ӌ(j��)
�����W(xu��)���^��l(f��)�F(xi��n)��ӑՓ�о����̎�����(d��o)����
�����������c(di��n)���y�c(di��n)
����1���̌W(xu��)���c(di��n)��ƽ�о��ȷ־��ζ���
����2���̌W(xu��)�y�c(di��n)��ƽ�о��ȷ־��ζ���
�����ġ��n�r(sh��)����
����l�n�r(sh��)
�����塢�̾ߌW(xu��)��
����Ӌ(j��)��C(j��)��ͶӰ�x���zƬ�����î��D����
����������������(d��ng)���(d��ng)�O(sh��)Ӌ(j��)
�����̎���(f��)��(x��)���룬�W(xu��)�����D̽��;������ͬ�w�{�Y(ji��)Փ;�̎�ʾ�����D���W(xu��)�����ݾ���(x��)
�����ߡ��̌W(xu��)���E
��������(f��)��(x��)�ᆖ(w��n)��
����1��ʲô��ƽ�о���ƽ�о���ʲô���|(zh��)��
����2��ʲô��ƽ����߅�Σ�ƽ����߅����ʲô���|(zh��)��
�������������n��
�����ɌW(xu��)����(d��ng)����һ��(sh��)�(y��n)��ÿ��(g��)ͬ�W(xu��)��һ���M�������^��M��֮�g��ʲô�P(gu��n)ϵ�����M���ǻ���ƽ�ȵģ���������֮�g�ľ��x����ȵģ���Ȼ���ڙM���Ϯ�һ�l��ֱ�ڙM����ֱ�� �������@�lֱ���������M���سɵĸ�������ʲô�P(gu��n)ϵ������ȣ���ʲô�����@�r(sh��)�ڙM�������ή�һ�l�c�M���ཻ��ֱ�� ���y(c��)�����������M���صõľ����Ƿ�Ҳ��ȣ�
����������(d��o)�W(xu��)��������(sh��)�(y��n)�ėl���͵õ��ĽY(ji��)Փ����һ��(g��)���}���̎����Y(ji��)���ɴ˵õ�ƽ�о��ȷ־��ζ�����
����ƽ�о��ȷ־��ζ��������һ�Mƽ�о���һ�lֱ���ϒ�õ�`������ȣ���ô������ֱ���Ͻصõľ���Ҳ��ȡ�
����ע�⣺�����еġ�һ�Mƽ�о���ָ����һ�M��������l����ƽ�о�����ÿ�����ɗlƽ�о��g�ľ��x����ȵ�����ƽ�о��M���@һ�c(di��n)���ʹ�W(xu��)�����_��
���������҂������lƽ�о�������(l��i)�C���@��(g��)�������ɌW(xu��)��������֪�����C����
������֪����D��ֱ�� �� ��
�������C�� ��
��������1����D����֪��ȵľ���ƽ�ƣ��cҪ���C�ăɗl���νM�������Σ�Ҳ�ɑ�(y��ng)��ƽ�о��g��ƽ�о�����ȵ� ����ͨ�^(gu��)ȫ�����������|(zh��)�����ɵõ�Ҫ�C�ĽY(ji��)Փ��
����������(d��o)�W(xu��)���ҳ���һ�N�C����
��������2��Ҫ�C�ăɗl���ηքe�����ε������҂�������ǰ�泣�õ��o�������������D(zhu��n)����ƽ����߅�κ������Σ�Ȼ���������@Щ��Ϥ��֪�R(sh��)�����C�� ��
�����C�����^(gu��) �c(di��n)�� �քe�� �� ���c(di��n) �� ���� �� ����D��
������
������ ��
������
�����֡� �� ��
������
������
������ʹ�W(xu��)����(du��)����������������գ���֪�R(sh��)�W(xu��)����W(xu��)���J(r��n)�R(sh��)�N������׃ʽ�D�Σ���D����Ӌ(j��)��C(j��)��(d��ng)�B(t��i)��ʾ����
��������(d��o)�W(xu��)���^���D�������� �У� �� ���t�ɵõ� ���ɴ˵ó���Փ 1��
������Փ1����(j��ng)�^(gu��)����һ�������c(di��n)�c��ƽ�е�ֱ������ƽ����һ����
����������(d��o)�W(xu��)���^���D���� �У� �� ���t�ɵõ� ���ɴ˵ó���Փ2��
������Փ2����(j��ng)�^(gu��)������һ߅�����c(di��n)�c��һ߅ƽ�е�ֱ����ƽ�ֵ���߅��
����ע�⣺��Փ1����Փ2Ҳ���Ǻ���Ҫ�Ķ������ڽ���Փ�C��Ӌ(j��)���н�(j��ng)���õ�����ˣ�Ҫ��W(xu��)��������պá�
��������(l��i)�v�������ƽ�о��ȷ־��ζ����(l��i)����ȷ�һ�l���Ρ�
������ ��֪����D������ ��
�������������� ����ȷ��c(di��n)��
���������������侀 ��
���������侀 ���������L(zh��ng)혴ν�ȡ ��
�������B�Y(ji��) ��
�������^(gu��)�c(di��n) �� �� �� �քe�� ��ƽ�о� �� �� �� ���քe�� ���c(di��n) �� �� �� ��
������ �� �� �����������ȷ��c(di��n)��
�������f(shu��)���ԣ��ɌW(xu��)���������ɣ�
���������Y(ji��)���U(ku��)չ��
�����Y(ji��)��
������l��ƽ�о��ȷ־��ζ�������Փ��
������2���������C��ֻȡ���lƽ�о��������^��(ji��n)�ε���r���C���ģ���(du��)�ڶ������l��ƽ�о�����r��Ҳ����ͬ�ӷ����C����
������3�������еġ�ƽ�о��M������ָÿ�����ɗlƽ�о��g�ľ��x����ȵ�����ƽ�о��M��
������4����(y��ng)�ö�������ȷ�һ�l���Ρ�
�����ˡ��������I(y��)
�����̲�P188��A�M2��9
�����š�����O(sh��)Ӌ(j��)
����ʮ���S�þ���(x��)
�����̲�P182��1��2
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ4
�����̌W(xu��)�΄�(w��)����
�����̌W(xu��)Ŀ��(bi��o)
����֪�R(sh��)����
����̽�����������ε����P(gu��n)����ͻ������|(zh��)��̽�����˽Ⲣ���յ������ε����|(zh��)��
������(sh��)�W(xu��)˼��
�����܉��\(y��n)�����ε����P(gu��n)��������|(zh��)�M(j��n)�����P(gu��n)��(w��n)�}��Փ�C��Ӌ(j��)�㣬�M(j��n)һ�����B(y��ng)�W(xu��)���ķ�����(w��n)�}������Ӌ(j��)��������
������Q��(w��n)�}
����ͨ�^(gu��)�����o�����������εĆ�(w��n)�}�D(zhu��n)����ƽ����߅�λ������Ά�(w��n)�}��ʹ�W(xu��)���w��(hu��)�D��׃�Q�ķ������D(zhu��n)����˼�룮
������БB(t��i)��
�����ڑ�(y��ng)�õ������ε����|(zh��)���^(gu��)���B(y��ng)�ɪ�(d��)��˼������(x��)�T�� �ڔ�(sh��)�W(xu��)�W(xu��)��(x��)���(d��ng)�Ы@�óɹ����w�(y��n)��
�������c(di��n)
�����������ε����|(zh��)���䑪(y��ng)�ã�
�����y�c(di��n)
������Q���Ά�(w��n)�}�Ļ����������������D(zhu��n)����ƽ����߅�κ������μ����_�\(y��n)���o�����������������P(gu��n)֪�R(sh��)�đ�(y��ng)�ã�
�����̌W(xu��)���̰���
�������(d��ng)���̈D
�������(d��ng)�ă�(n��i)�ݺ�Ŀ��
�������(d��ng)1��һ��
�������(d��ng)2�f(shu��)һ�f(shu��)
�������(d��ng)3��һ��
�������(d��ng)4������
�������(d��ng)5��һ��
�������(d��ng)6��һ��
�����^�����ΈDƬ�����뱾��(ji��)�n�ČW(xu��)��(x��)��(n��i)�ݣ�
�����˽����ζ��x�����������Q�����
����ͨ�^(gu��)���D���(d��ng)�������l(f��)�F(xi��n)�����c�����ε��D(zhu��n)���P(gu��n)ϵ��
����̽���õ��������ε�.���|(zh��)��
����ͨ�^(gu��)��Q���w��(w��n)�}�����ҽ�Q���Ά�(w��n)�}�ķ�����
����ͨ�^(gu��)�������얹�֪�R(sh��)������������B˼�룮
�����̌W(xu��)�^(gu��)���O(sh��)Ӌ(j��)
������(w��n)�}�c�龰
����������
�����O(sh��)Ӌ(j��)��D
����[���(d��ng)1]
�����^���D�У�������Ϥ�ĈD�Ά������ʲô��ͬ�����c(di��n)��
������ʾ�DƬ���W(xu��)�����p��
�����Y(ji��)�ψDƬ���̎�����(d��o)�W(xu��)��ע���@Щ�DƬ�Ĺ�ͬ������һ�M��(du��)߅ƽ�ж���һ�M��(du��)߅��ƽ�У�
�����ɬF(xi��n)��(sh��)�Ќ�(sh��)�H��(w��n)�}���֣��O(sh��)�Æ�(w��n)�}�龳���������n���}��ͨ�^(gu��)�W(xu��)���^��DƬ�͚w�{�D�ε����c(di��n)�����B(y��ng)�W(xu��)�����^�졢����������
����[���(d��ng)2]
�������ζ��x һ�M��(du��)߅ƽ�ж���һ�M��(du��)߅��ƽ�е���߅�ν������Σ�
�����W(xu��)������(j��)���θ�����D�Σ��̎������M(j��n)һ������(d��o)�W(xu��)��������cƽ����߅�εą^(q��)�e��(li��n)ϵ��
����ͨ�^(gu��)ȣ����B(y��ng)�W(xu��)���w�{�����Y(ji��)��������
������(w��n)�}�c�龰
����������
�����O(sh��)Ӌ(j��)��D
����һЩ��������
������1������D�����ס������ߣ�
������2���������Σ�������ȵ����ν����������Σ�
������3��ֱ�����Σ���һ��(g��)����ֱ�ǵ����ν���ֱ�����Σ�
�����W(xu��)����С�W(xu��)�ѽ�(j��ng)��(du��)������һ���ĸ����J(r��n)�R(sh��)����˽̎��W(xu��)���Լ���B��1���еĻ���������� (t��ng)�W(xu��)���l(f��)�Ժ� �̎����ԏ�(qi��ng)�{(di��o)���������c��߅�ε��P(gu��n)ϵ��
�������ϡ��µĸ������ɵ��L(zh��ng)�́�(l��i)���x�ģ���������ָλ�Á�(l��i)�f(shu��)�ģ�
������Ϥ�D�Σ����_�����̽���D�����|(zh��)����(zh��n)�䣮
����[���(d��ng)3]
������һ��
�������������o�D�е�ÿ��(g��)�������Ю�һ�l���Σ�
������1�����Ӯ����ܵõ�һ��(g��)���Σ�
������2������Щ�������У��܉�õ�һ��(g��)�������Σ�
�����ڌW(xu��)����(d��)��̽���Ļ��A(ch��)�ϣ��W(xu��)���ֽM������
�����̎����cС�M���(d��ng)��ָ��(d��o)���A (t��ng)�W(xu��)��������ᘌ�(du��)��ͬ�J(r��n)�R(sh��)ˮƽ�ČW(xu��)��������(d��o)�����_���D��
�������λ��(d��ng)�̎���(y��ng)���c(di��n)�P(gu��n)ע��
������1���W(xu��)���ڻ��(d��ng)�^(gu��)�����ܷ�l(f��)�F(xi��n)�����c������֮�g��(li��n)ϵ������֮�g���D(zhu��n)��������
������2���W(xu��)���ܷ����������D(zhu��n)����������Σ�
������3���W(xu��)���ܷ�����(d��ng)���c̽�����(d��ng)����ӑՓ�аl(f��)���Լ���Ҋ(ji��n)�⣬�A (t��ng)���˵���Ҋ(ji��n)����(du��)��ͬ���^�c(di��n)�M(j��n)���|(zh��)�ɣ����Ы@�森
�����������ε����|(zh��)�c������������£�����ڻ��(d��ng)3���O(sh��)Ӌ(j��)�˵ڣ�2���}�����ƌ�(d��o)�����������|(zh��)����Ҫ�����o�����r(sh��)�����Խ�������������(l��i)�о��������Ǹ���(j��)�������������S��(du��)�Q�D�Σ��ɵõ������������S��(du��)�Q�D���@�l���|(zh��)������(d��ng)4�N�_(k��i)չ̽���춨�˻��A(ch��)��
������(w��n)�}�c�龰
����������
�����O(sh��)Ӌ(j��)��D
����[���(d��ng)4]
����������
����̽���������ε����|(zh��)���������S��(du��)�Q��Q��(w��n)�}��˼�룩��
������һ����������һ��(g��)�������Σ��B�Ӄɗl��(du��)�Ǿ���
������1���@��(g��)�D�����S��(du��)�Q�D�Ά��(du��)�Q�S��������ܰl(f��)�F(xi��n)��Щ��ȵľ��κ���ȵĽǣ��W(xu��)�����D��ͨ�^(gu��)�^����룻
������2���@��(g��)�������εăɗl��(du��)�Ǿ����L(zh��ng)����ʲô�P(gu��n)ϵ��
�����W(xu��)�����Ռ�(sh��)�(y��n)���E����(d��)����ɮ��D�^(gu��)�̣��^��D�Σ�˼���̎�����Ć�(w��n)�}�����롢�(y��n)�C���w�{�Y(ji��)Փ��
����ᘌ�(du��)��ͬ�J(r��n)�R(sh��)ˮƽ�ČW(xu��)�����̎�ָ��(d��o)�W(xu��)�����(d��ng)��
����������ͬ�w�{��
�����ٵ����������S��(du��)�Q�D�Σ����µ����c(di��n)�B���nj�(du��)�Q�S��
�����ڵ�����������ȣ�
�����۵�������ͬһ���ϵăɂ�(g��)����ȣ�
�����ܵ������εăɗl��(du��)�Ǿ���ȣ�
�����̌W(xu��)��Ҫע������(d��o)�W(xu��)���C���������ε����|(zh��)���������C������������ͬһ���ϵăɂ�(g��)����ȡ��@�l���|(zh��)�r(sh��)����ƽ�������͡����ߡ��@�ɷN��Ҋ(ji��n)���o�������ڽ̌W(xu��)���^һ�γ��F(xi��n)�����Խ�˙C(j��)��(hu��)���o�W(xu��)����B�@�ɷN�o���������ӷ�����
����[���(d��ng)5]
����������
������1 ���̲�P118����1���ԣ�
������2 ��D������ABCD��AD��BC��
������B=70�㣬��C=40�㣬AD=6cm��BC=15cm��
������CD���L(zh��ng)��
����������ͬ���������ҽ�Q��(w��n)�}�ķ����Ͳ��ԣ�
������1�ǵ����������|(zh��)��ֱ���\(y��n)�ã�Ո(q��ng)�W(xu��)����������𣬽̎��� (t��ng)��ͬ�r(sh��)ע��ָ��(d��o)�W(xu��)�������C����EAD�ǵ��������Εr(sh��)��Ҫ�õ����εĶ��x�����µ���ƽ�У�AD��BC�����@һ�c(di��n)��
�����������O(sh��)������֪�����o�ėl�����Ƶ�һ��(g��)�������У�����Խ�Q��(w��n)�}��
�����䷽���ǣ�ƽ��һ�����^(gu��)�c(di��n)A��AE��DC��BC��E�������߅��AECD��ƽ����߅�Σ�����֪�ֿ��Եõ���ABE�ǵ��������Σ�EA=EB�������CD=EA=EB=BC��EC=BC��AD=9cm��
�����⣺���ԣ�
����ͨ�^(gu��)�}Ŀ�ľ���(x��)�c�v�⑪(y��ng)�W(xu��)��֪������Q���Ά�(w��n)�}�Ļ���˼��ͷ�������ͨ�^(gu��)�����m��(d��ng)?sh��)��o�����������Ά�(w��n)�}�D(zhu��n)�����ѽ�(j��ng)��Ϥ��ƽ����߅�κ������Ά�(w��n)�}��(l��i)��Q���ڽ̌W(xu��)�r(sh��)��(y��ng)�W(xu��)��ע�����������ã������@Щ�o������ʹ�Ì�(du��)�ڌW(xu��)������(n��i)�ݺ��Ў�����
������(w��n)�}�c�龰
����������
�����O(sh��)Ӌ(j��)��D
������3��֪����D��������ABCD�У�AD��BC����D��90�㣬��CAB����ABC��
����BE��AC��E��
�������C��BE��CD��
����������Ҫ�CBE=CD���������m��(d��ng)?sh��)��o��������(g��u)��ȫ�������Σ��䷽���ǣ�ƽ��һ�����^(gu��)�c(di��n)D��DF��AB��BC��F�������߅��ABFD��ƽ����߅�Σ��tDF=AB������֪�Ɍ�(d��o)����DFC=��BAE�����Rt��ABE��Rt��FDC��AAS�����ʿɵó�BE=CD��
�����C�����ԣ�
������2�c��3�@��o�����o�������ǡ�ƽ��һ�������ώ���?c��)ڽ̌W(xu��)����(x��)�п��Ը���(j��)�W(xu��)���Č�(sh��)�H��r��������(d��o)���a(b��)�������o���������ӷ������W(xu��)�����˽⡢��Ҋ(ji��n)�R(sh��)��
����[���(d��ng)6]
����1���Y(ji��)
����2���������I(y��)
������1����֪�������ε��J�ǵ���60�����ăɵքe��15cm��49cm�����������L(zh��ng)����e��
������2����֪����D��
��������ABCD��CD//AB������
�������C��AD=AB��DC��
������3����֪����D��
��������ABCD�У�AD��BC��E��AB�����c(di��n)��DE��CE�����C��AD+BC=DC�������L(zh��ng)DE��CB���L(zh��ng)�����c(di��n)F����ȫ�ȿɵýY(ji��)Փ��
���������w�{���Y(ji��)��
������Q���Ά�(w��n)�}���õķ�����
������1����ƽ�������������ηֳ�һ��(g��)ƽ����߅�κ�һ��(g��)�����Σ��D1����
������2�������ߡ���ʹ�����ڃɂ�(g��)ֱ���������У��D2����
������3��������������(g��u)����й����ǵăɂ�(g��)���������Σ��D3����
������4����ƽ�ƌ�(du��)�Ǿ�����ʹ�ɗl��(du��)�Ǿ���ͬһ��(g��)�������У��D4����
������5�����ȷe׃�Ρ����B�Y(ji��)�����ϵ�һ���c(di��n)����һ�����c(di��n)�������L(zh��ng)�c�µ����L(zh��ng)������һ�c(di��n)����(g��u)�������Σ��D5����
�����M������W(xu��)�����c�l(f��)����һ��(g��)�������^(gu��)�̣�
������������(ji��)�n��(y��ng)���^(gu��)���o�������ӷ������ȿ���呟��W(xu��)��˼�S���ֿ������o�W(xu��)���^�m(x��)̽���Ŀ��g��
�����W(xu��)��ͨ�^(gu��)��(d��)��˼��������n�����I(y��)�����ڰl(f��)�F(xi��n)��(w��n)�}�����r(sh��)��©�a(b��)ȱ��
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ5
����֪�R(sh��)����
����1.�˽�ɂ�(g��)�D�γ��S��(du��)�Q�Ե����|(zh��)���˽��S��(du��)�Q�D�ε����|(zh��)��
����2.̽�����δ�ֱƽ�־������|(zh��)��
�����^(gu��)�̷���
����1.��(j��ng)�v̽���S��(du��)�Q�D�����|(zh��)���^(gu��)�̣��M(j��n)һ���w�(y��n)�S��(du��)�Q�����c(di��n)���l(f��)չ���g�^�졣
����2.̽�����δ�ֱƽ�־������|(zh��)�����B(y��ng)�W(xu��)���J(r��n)��̽�����e�O˼����������
������БB(t��i)�ȃr(ji��)ֵ�^ͨ�^(gu��)��(du��)�S��(du��)�Q�D�����|(zh��)��̽������ʹ�W(xu��)����(du��)�S��(du��)�Q���˸��M(j��n)һ�����J(r��n)�R(sh��)�����(d��ng)�c̽�����^(gu��)�̿��Ը���̶ȵؼ��l(f��)�W(xu��)���W(xu��)��(x��)������(d��ng)�Ժͷe�O�ԣ���ʹ�W(xu��)������һЩ�����о���(w��n)�}��������
�����̌W(xu��)���c(di��n)
����1.�S��(du��)�Q�����|(zh��)��
����2.���δ�ֱƽ�־������|(zh��)��
�����̌W(xu��)�y�c(di��n)�w�(y��n)�S��(du��)�Q��.������
�����̌W(xu��)�������ֶζ�ý�w�̌W(xu��)
�����^(gu��)�̽̌W(xu��)��(n��i)��
���������������
���������D�Ό�(du��)�Q�����|(zh��)��һ���ß�Ƭ
�����Ϲ�(ji��)�n�҂���ͬ̽ӑ���S��(du��)�Q�D�Σ�֪���F(xi��n)��(sh��)�������������S��(du��)�Q�D�Σ���ʹ������dz���������ô�҂������^�m(x��)��(l��i)�о��S��(du��)�Q�����|(zh��)��
�����ß�Ƭ��
����1���D�еČ�(du��)�Q�c(di��n)����Щ?
����2���c(di��n)A��A���B���cֱ��MN��ʲô�ӵ��P(gu��n)ϵ?
��������?����ABC�c��ABC�P(gu��n)��ֱ��MN��(du��)�Q���c(di��n)A��B��C�քe���c(di��n)A��B��C�Č�(du��)�Q�c(di��n)���O(sh��)AA����(du��)�Q�SMN���c(di��n)P������ABC�͡�ABC��MN��(du��)�ۺ��c(di��n)A�cA�غϣ�������AP=AP��MPA=MPA=90������AA��BB��CC�cMN���˴�ֱ���⣬MN߀��(j��ng)�^(gu��)����AA��BB��CC�����c(di��n)��
�����҂��ѽ�(j��ng)�^(gu��)�������c(di��n)���Ҵ�ֱ���@�l���ε�ֱ���������@�l���εĴ�ֱƽ�־���
�������x����(j��ng)�^(gu��)���ε����c(di��n)���Ҵ�ֱ���@�l���Σ��ͽ��@�l���εĴ�ֱƽ�־���Ҳ���д�����
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ6
�����n�r(sh��)Ŀ��(bi��o)
����1�����շ�ʽ������ʽ�ĸ��
����2�����շ�ʽ�Ƿ������x����ʽ��ֵ�Ƿ��������R(sh��)�e������
�����̌W(xu��)���c(di��n)
�������_�����ʽ�����x����ʽ�Ƿ������x�ėl������ʽ��`ֵ����ėl����
�����̌W(xu��)�y�c(di��n)��
�������_�����ʽ�����x����ʽ�Ƿ������x�ėl������ʽ��ֵ����ėl����
�����̌W(xu��)�r(sh��)�g��һ�n�r(sh��)��
�����̌W(xu��)�þߣ�ͶӰ�x�ȡ�
�����̌W(xu��)�^(gu��)�̣�
����һ����(f��)��(x��)�ᆖ(w��n)
����1��ʲô����ʽ��ʲô�dž��(xi��ng)ʽ��ʲô�Ƕ��(xi��ng)ʽ��
����2���Д����и�ʽ�У���Щ����ʽ����Щ������ʽ��
�����٣�m2 ��1��x��y2�� �� ��
������ �� ��
�����������n�v�⣺
�����O(sh��)��(w��n)����������ʽ���У�����ʽ��ʲô�^(q��)�e��
����С�Y(ji��)��1����ʽ�ĸ��һ��أ������ʽ�ӽ�����ʽ������A��B������ʽ��B�к�����ĸ��
��������(x��)�����и�ʽ�У���Щ�Ƿ�ʽ��Щ���ǣ�
������1��������2������3������4������5��x2����6����4
������(qi��ng)�{(di��o)����6����4�����ǟo(w��)��ʽ��������ʽ���ʲ��Ƿ�ʽ��
����2��С�Y(ji��)����(du��)��ʽ����ʽ�����_�^(q��)�e����ʽ�ķ��Ӻͷ�ĸ������ʽ�����ӿ��Ժ�����ĸ��Ҳ���Բ�������ĸ������ĸ�б�횺�����ĸ���@�Ƿ�ʽ�c��ʽ�ĸ����^(q��)�e��
��������(x��)���n����(x��)P6����(x��)1��2�}
�����O(sh��)��(w��n)�����W(xu��)�����n����P5��˼�������֣�Ȼ��ش���(w��n)�}����
�������}�v�⣺�n��P5���}1
��������������ʽ�еķ�ĸ�ǣ���1��3x��2��x-1��3��5-3b��4��x-y��ֻҪ�@�����ĸ�����㣬��ʽ�������x��
������������}�^(gu��)�̡���
����3��С�Y(ji��)����ʽ�Ƿ������x���R(sh��)�e��������(d��ng)��ʽ�ķ�ĸ����r(sh��)����ʽ�o(w��)���x����(d��ng)��ʽ�ķ�ĸ��������r(sh��)����ʽ�����x��
�����������}����(d��ng)xȡʲôֵ�r(sh��)����ʽ�����x��
�����⣺�ɷ�ĸx2��4=0����x=��2��
������ ��(d��ng)x�١�2�r(sh��)����ʽ�����x��
�����O(sh��)��(w��n)��ʲô�r(sh��)���ʽ��ֵ�����أ�
��������
�����⣺��(d��ng) �� ��ʽ��ֵ����
���꼉(j��)��(sh��)�W(xu��)�̰� ƪ7
����һ��֪�R(sh��)�c����
����1���ĬF(xi��n)��(sh��)�龳�����е�֪�R(sh��)����(j��ng)�(y��n)���l(f��)��ӑՓ�ɂ�(g��)׃��֮�g�������P(gu��n)ϵ�����(du��)����(sh��)������(sh��)��������⣮
����2����(j��ng)�v����������(sh��)������^(gu��)�̣��I(l��ng)��(hu��)����������(sh��)�����x�����ⷴ��������(sh��)�ĸ��
���������^(gu��)���c����
����1����(j��ng)�v��(du��)�ɂ�(g��)׃��֮�g�����P(gu��n)ϵ��ӑՓ�����B(y��ng)�W(xu��)���ı�eΨ�����x�^�c(di��n)��
����2����(j��ng)�v����������(sh��)������^(gu��)�̣��l(f��)չ�W(xu��)���ij���˼�S��������ߔ�(sh��)�W(xu��)�����R(sh��)��
����������БB(t��i)���c�r(ji��)ֵ�^
����1����(j��ng)�v����������(sh��)������^(gu��)�̣��w��(hu��)��(sh��)�W(xu��)�W(xu��)��(x��)����Ҫ�ԣ���ߌW(xu��)���ČW(xu��)��(x��)��(sh��)�W(xu��)���dȤ��
����2��ͨ�^(gu��)�ֽMӑՓ�����B(y��ng)�W(xu��)�������������R(sh��)��̽������
�����̌W(xu��)���c(di��n)��������I(l��ng)��(hu��)����������(sh��)�ĸ��
�����̌W(xu��)�y�c(di��n)���I(l��ng)�����ĸ��
�����̌W(xu��)�^(gu��)����
����һ����(chu��ng)�O(sh��)�龳����(d��o)�����n
�������(d��ng)1
������(w��n)�}�����І�(w��n)�}�У�׃���g�Č�(du��)��(y��ng)�P(gu��n)ϵ�������ӵĺ���(sh��)�P(gu��n)ϵʽ��ʾ���@Щ����(sh��)��ʲô��ͬ���c(di��n)��
����(1)�������F·ȫ�̞�1463km������ij����܇���Õr(sh��)�gt����λ��h���Sԓ��܇ƽ���ٶ�v����λ��km/h����׃����׃����
����(2)ijסլС�^(q��)Ҫ�Nֲһ��(g��)��e��1000m2�ľ��β�ƺ����ƺ���L(zh��ng)��y�S��x��׃����
����(3)��֪�����еĿ���e��1.68��104ƽ��ǧ�ף��˾�ռ��������eS����λ��ƽ��ǧ��/�ˣ��Sȫ���˿�n����λ���ˣ���׃����׃����
���������О飺
�������W(xu��)���M(j��n)��С�M�������������M(j��n)��ȫ���ԵĆ�(w��n)�����.�W(xu��)�����Լ����Z(y��)���f(shu��)���ɂ�(g��)׃���g���P(gu��n)ϵ��ʲô���Կ�������(sh��)���˽���ӑՓ�ĺ���(sh��)�ı��_(d��)��ʽ��
�����̎��M���W(xu��)��ӑՓ���ᆖ(w��n)�W(xu��)������������(d��ng)��
�����ڴ˻��(d��ng)���ώ���(y��ng)���c(di��n)�P(gu��n)ע�W(xu��)����
�������ܷ�e�O����(d��ng)�غ���������
�������ܷ����Z(y��)���f(shu��)���ɂ�(g��)׃���g���P(gu��n)ϵ��
�������ܷ��˽���ӑՓ�ĺ���(sh��)���_(d��)��ʽ���γɷ���������(sh��)����ľ��w����
������������𣺣�1��
��������2��
��������3��
��������v����׃����t��v��'����(sh��)��x����׃����y��x�ĺ���(sh��)��n����׃����s��n�ĺ���(sh��)��
��������ĺ���(sh��)�P(gu��n)ϵʽ��������
��������ʽ������k�dz���(sh��)��
��������(li��n)ϵ����S��(li��n)��
�������(d��ng)2
�������І�(w��n)�}�У�׃���g�Č�(du��)��(y��ng)�P(gu��n)ϵ�����@�ӵĺ���(sh��)ʽ��ʾ��
������1��һ��(g��)��Ӿ�ص��ݷe��20xxm3��ע�M��Ӿ�����õĕr(sh��)�g�Sעˮ�ٶ�u��׃����׃����
������2��ij�����w���w�e��1000cm3�������w�ĸ�h(yu��n)�S����eS��׃����׃����
������3��һ��(g��)���w��100ţ�D�����w��(du��)����ĉ���p�S���w�c����Ľ��|��eS��׃����׃����
����������
�����W(xu��)���Ȫ�(d��)��˼�������M(j��n)��ȫ�ཻ����
�����̎������n���������(w��n)�}���P(gu��n)ע�W(xu��)��˼�����^(gu��)�̣��ڴ˻��(d��ng)�У��̎���(y��ng)���c(di��n)�P(gu��n)ע�W(xu��)����
����(1)�ܷ�ĬF(xi��n)��(sh��)�龳�г�����ɂ�(g��)׃���ĺ���(sh��)�P(gu��n)ϵ��
����(2)�ܷ�e�O����(d��ng)���cС�M���(d��ng)��
����(3)�ܷ���^��̵��I(l��ng)��(hu��)����(sh��)������������(sh��)�ĸ��
������������𣺣�1��
��������2��
��������3��
�����������ɂ�(g��)׃��x��y֮�g���P(gu��n)ϵ���Ա�ʾ��
��������ʽ����ôy��x�ķ���������(sh��)������������(sh��)����׃��x���ܞ��㣮
�������(d��ng)3
������һ����
����һ��(g��)���ε���e��20cm2�� �����ăɗl߅�L(zh��ng)��xcm��ycm����ô׃��y��׃��x�ĺ���(sh��)��Ƿ���������(sh��)���ʲô��
���������О飺
�����W(xu��)�����M(j��n)�Ъ�(d��)��˼�������M(j��n)��ȫ�ཻ�����̎������(w��n)�}���P(gu��n)ע�W(xu��)��˼�����˻��(d��ng)�н̎���(y��ng)���c(di��n)�P(gu��n)ע��
���������ܷ����ⷴ��������(sh��)�����x�����ⷴ��������(sh��)�ĸ��
�����ڌW(xu��)���ܷ��������������(sh��)��ģ�ͣ�
�����یW(xu��)���ܷ�e�O����(d��ng)�غ�����������
�������(d��ng)4
������(w��n)�}1�������Ă�(g��)��ʽ�е�y��x�ķ���������(sh��)��
������(w��n)�}2����֪y��x�ķ���������(sh��)����(d��ng)x=2�r(sh��)��y=6
����(1)����y�cx�ĺ���(sh��)�P(gu��n)ϵʽ��
����(2)��(d��ng)x=4�r(sh��)��y��ֵ��
���������О飺
�����W(xu��)����(d��)��˼����Ȼ��С�M�����������̎�Ѳҕ���鿴�W(xu��)����ɵ���r�����o�輰�r(sh��)����(d��o)���ڴ˻��(d��ng)�н̎���(y��ng)���c(di��n)�P(gu��n)ע��
�����ٌW(xu��)���ܷ��I(l��ng)��(hu��)����������(sh��)�����x�����ⷴ��������(sh��)�ĸ��
�����ڌW(xu��)���ܷ�e�O����(d��ng)���cС�M���(d��ng)��
�������������
����1��ֻ��xy=123�Ƿ���������(sh��)��
����2����������?y��n)�y��x�ķ���������(sh��)������
�������ٰ�x=2��y=6������ʽ�Ϳ��������(sh��)k��ֵ��
�����⣺��1���O(sh��)
��������?y��n)�x=2�r(sh��)��y=6��������
�������k=12
�������
������2����x=4����
��������
��������얹����
�������(d��ng)5
����1����֪y��x�ķ���������(sh��)�����Ү�(d��ng)x=3�r(sh��)��y=8��
������1������y�cx֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��
������2����y=2�r(sh��)x��ֵ��
����2��y��x�ķ���������(sh��)���±��o����x�cy��һЩֵ��
������1�������@��(g��)����������(sh��)�ı��_(d��)ʽ��
������2������(j��)����(sh��)���_(d��)ʽ����ϱ���
�����W(xu��)����(d��)������(x��)���������cͬ�����������v�_(t��i)��ʾ���̎�Ҫ���c(di��n)�P(gu��n)ע���W(xu��)��������
�����ġ��n�r(sh��)С�Y(ji��)
��������������(sh��)�����γɵ��^(gu��)���У���ҳ���������е����(j��ng)�(y��n)�ͱ���֪�R(sh��)��ע���ھ�(w��n)�}��׃���������P(gu��n)ϵ��׃��Ҏ(gu��)�ɣ��������⣮�ڸ�����γ��^(gu��)���У��ĸ����J(r��n)�R(sh��)�����l(f��)�J(r��n)�R(sh��)һ������������є[Ó��ԭ�ͳɞ锵(sh��)�W(xu��)��(du��)����������(sh��)�����S���Ĕ�(sh��)�W(xu��)���x��ͨ�^(gu��)�e�����f(shu��)����ӑՓ�Ȼ��(d��ng)����֪��(sh��)�W(xu��)�۹⣬��ҕijЩ��(sh��)�H�F(xi��n)��
�����꼉(j��)��(sh��)�W(xu��)�̰������P(gu��n)���£�
���꼉(j��)�Ĕ�(sh��)�W(xu��)�̰�12-14
���꼉(j��)��(sh��)�W(xu��)�̰�06-18
���꼉(j��)��(sh��)�W(xu��)�̰������T��12-03
���������꼉(j��)��(sh��)�W(xu��)�̰�12-04
���꼉(j��)��(sh��)�W(xu��)�̰�������12-04
���꼉(j��)��(sh��)�W(xu��)�̰����]��12-06
�����]�����꼉(j��)��(sh��)�W(xu��)�̰�12-05
���꼉(j��)��(sh��)�W(xu��)�̰������]��12-04